题目内容
3. 如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.
如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.(Ⅰ)求二面角F-DE-C的大小;
(Ⅱ)若在平面DEF上存在点P,使得BP⊥平面DEF,试通过计算说明点P的位置.
分析 (Ⅰ)以A为原点,AD为x轴,AB为y轴,AF为z轴,建立空间直角坐标系,利用向量法能求出二面角F-DE-C的大小.
(Ⅱ)设$\overrightarrow{DP}$=$λ\overrightarrow{DE}+μ\overrightarrow{DF}$,推导出$\overrightarrow{BP}$=$\overrightarrow{BD}+\overrightarrow{DP}$=(2-2λ-2μ,2λ-2,2λ+μ),由线面垂直的性质能求出P是线段DE上靠近E的三等分点.
解答 解:(Ⅰ)∵底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,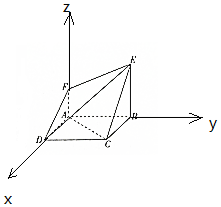
∴AF⊥底面ABCD,
以A为原点,AD为x轴,AB为y轴,AF为z轴,建立空间直角坐标系,
∵DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2,
∴D(2,0,0),E(0,2,2),F(0,0,1),C(2,2,0),
$\overrightarrow{DE}$=(-2,2,2),$\overrightarrow{DF}$=(-2,0,1),$\overrightarrow{DC}$=(0,2,0),
设平面DEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=-2x+2y+2z=0}\\{\overrightarrow{n}•\overrightarrow{DF}=-2x+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-1,2),
设平面DEC的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DE}=-2a+2b+2c=0}\\{\overrightarrow{m}•\overrightarrow{DC}=2b=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,0,1),
设二面角F-DE-C的大小为θ,由图形知θ为钝角,
则cosθ=-$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=-$\frac{3}{\sqrt{6}•\sqrt{2}}$=-$\frac{\sqrt{3}}{2}$,
∴θ=$\frac{5π}{6}$,
∴二面角F-DE-C的大小为$\frac{5π}{6}$.
(Ⅱ)设$\overrightarrow{DP}$=$λ\overrightarrow{DE}+μ\overrightarrow{DF}$,
∵$\overrightarrow{DE}=(-2,2,2)$,$\overrightarrow{DF}$=(-2,0,1),
又$\overrightarrow{BD}$=(2,-2,0),$\overrightarrow{DP}$=$λ\overrightarrow{DE}$+μ$\overrightarrow{DF}$=(-2λ,2λ,2λ)+(-2μ,-2μ,2λ,2λ+μ),
∴$\overrightarrow{BP}$=$\overrightarrow{BD}+\overrightarrow{DP}$=(2-2λ-2μ,2λ-2,2λ+μ),
∵$\left\{\begin{array}{l}{\overrightarrow{BP}•\overrightarrow{DP}=0}\\{\overrightarrow{BP}•\overrightarrow{DE}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{-2(2-λ-2μ)+2λ+μ=0}\\{-2(2-2λ-2μ)+2(2λ-2)+2(2λ+μ)=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{μ=0}\\{λ=\frac{2}{3}}\end{array}\right.$,即$\overrightarrow{DP}$=$\frac{2}{3}\overrightarrow{DE}$.
∴P是线段DE上靠近E的三等分点.
点评 本题考查二面角的求法,考查满足条件的点的位置的确定,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 车流量x(万辆/小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5浓度y(微克/立方米) | 30 | 36 | 38 | 40 | 42 | 44 | 50 |
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时PM2.5的浓度;(II)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
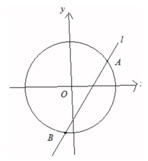 已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.
已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.