题目内容
16.已知双曲线$\frac{x^2}{25}-\frac{y^2}{9}=1$上有一点M到左焦点F1的距离为18,则点M到右焦点F2的距离是( )| A. | 8 | B. | 28 | C. | 12 | D. | 8或28 |
分析 求得双曲线的a,b,c,运用双曲线的定义,可得||MF1|-|MF2||=2a=10,解方程可得所求值,检验M在两支的情况即可.
解答 解:双曲线$\frac{x^2}{25}-\frac{y^2}{9}=1$的a=5,b=3,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{34}$,
由双曲线的定义可得||MF1|-|MF2||=2a=10,
即为|18-|MF2||=10,解得|MF2|=8或28.
检验若M在左支上,可得|MF1|≥c-a=$\sqrt{34}$-5,成立;
若M在右支上,可得|MF1|≥c+a=$\sqrt{34}$+5,成立.
故选:D.
点评 本题考查双曲线的定义、方程和性质,主要是定义法的运用,注意检验M的位置,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
7.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{4}=1$过点(2,-1),则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
4.已知R为实数集,集合A={x|x2-2x≥0},B={x|x>1},则(∁RA)∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
1.已知向量$\overrightarrow{m}$=(-1,2),$\overrightarrow{n}$=(1,λ),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则$\overrightarrow{m}$+2$\overrightarrow{n}$与$\overrightarrow{m}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
8.已知函数$f(x)=2sin({ωx+φ})+1({ω>0,|φ|<\frac{π}{2}}),f(α)=-1,f(β)=1$,若|α-β|的最小值为$\frac{3π}{4}$,且f(x)的图象关于点$({\frac{π}{4},1})$对称,则函数f(x)的单调递增区间是( )
| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
5.△ABC中,角A,B,C的对边分别为a,b,c,若a=$\frac{\sqrt{6}}{2}$b,A=2B,则cosB 等于( )
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{6}}{5}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
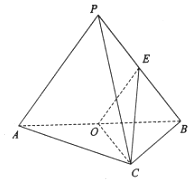 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.