题目内容
4．设奇函数f（x）在区间[-7，-3]上是减函数且最小值为-6，函数g（x）=$\frac{ax+1}{x+2}$，其中a＜$\frac{1}{2}$．（1）判断函数g（x）在（-2，+∞）上的单调性，并用定义法证明；
（2）求函数F（x）=f（x）+g（x）在区间[3，7]上的最大值．
分析 （1）根据函数单调性的定义证明即可；（2）分别求出f（x）和g（x）的最大值，求出F（x）的最大值即可．
解答 解：（1）函数g（x）在（-2，+∞）上是减函数，
证明如下：
设-2＜x1＜x2，
∵g（x）=a+$\frac{1-2a}{x+2}$，
∴g（x2）-g（x1）
=（a+$\frac{1-2a}{{x}_{2}+2}$ ）-（a+$\frac{1-2a}{{x}_{1}+2}$）
=（1-2a）•$\frac{{{x}_{1}-x}_{2}}{{（x}_{2}+2）{（x}_{1}+2）}$，
∵-2＜x1＜x2，
∴$\frac{{{x}_{1}-x}_{2}}{{（x}_{2}+2）{（x}_{1}+2）}$＜0，
∵a＜$\frac{1}{2}$，∴g（x2）＜g（x1），
∴a＜$\frac{1}{2}$时，g（x）在（-2，+∞）递减；
f（x）min=f（-3）=-6，且f（x）是奇函数，
∴f（3）=6，即f（x）在区间[3，7]上的最大值是6，
由（1）得：g（x）在[3，7]上也是减函数，
∴F（x）max=f（3）+g（3）=6+$\frac{3a+1}{3+2}$=$\frac{3a+31}{5}$．
点评 本题考查了函数单调性的证明，考查函数的单调性、最值问题，是一道中档题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
8．已知函数$f（x）=2sin（{ωx+φ}）+1（{ω＞0，|φ|＜\frac{π}{2}}），f（α）=-1，f（β）=1$，若|α-β|的最小值为$\frac{3π}{4}$，且f（x）的图象关于点$（{\frac{π}{4}，1}）$对称，则函数f（x）的单调递增区间是（ ）
| A． | $[{-\frac{π}{2}+2kπ，π+2kπ}]，k∈Z$ | B． | $[{-\frac{π}{2}+3kπ，π+3kπ}]，k∈Z$ | ||
| C． | $[{π+2kπ，\frac{5π}{2}+2kπ}]，k∈Z$ | D． | $[{π+3kπ，\frac{5π}{2}+3kπ}]，k∈Z$ |
9．如图，在△ABC中，N、P分别是AC、BN的中点，设$\overrightarrow{BA}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，则$\overrightarrow{AP}$=（ ）
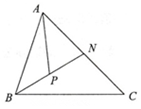
| A． | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B． | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C． | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D． | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |
16．已知函数f（x）=sin（ωx+φ）（ω＞，|φ|＜$\frac{π}{2}$），其图象相邻两个对称中心的距离为$\frac{π}{2}$，且f（x+$\frac{π}{6}$）=f（-x），下列判断正确的是 （ ）
| A． | 函数f（x）的最小正周期为2π | |
| B． | 函数f（x）的图象关于点（$\frac{7π}{12}$，0）对称 | |
| C． | 函数f（x）在[$\frac{3π}{4}$，π]上单调递增 | |
| D． | 函数f（x）的图象关于直线x=-$\frac{7π}{12}$对称 |