题目内容
a,b,c表示不同直线,M表示平面,给出四个命题:
①若a∥M,b∥M,则a∥b或a,b相交或a,b异面;
②若b?M,a∥b,则a∥M;
③a⊥c,b⊥c,则a∥b;
④a⊥M,b⊥M,则a∥b.
其中正确命题为( )
①若a∥M,b∥M,则a∥b或a,b相交或a,b异面;
②若b?M,a∥b,则a∥M;
③a⊥c,b⊥c,则a∥b;
④a⊥M,b⊥M,则a∥b.
其中正确命题为( )
| A、①④ | B、②③ | C、③④ | D、①② |
考点:空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:阅读型,空间位置关系与距离
分析:根据线面平行的性质即可判断①;由线面平行的判断定理即可判断②;通过举反例,结合两直线的位置关系即可判断③;由线面垂直的性质定理:垂直于同一平面的两直线平行,即可判断④.
解答:
解:①若a∥M,b∥M,则a∥b或a,b相交或a,b异面,故①正确;
②若b?M,a∥b,a?M,则a∥M,故②错;
③a⊥c,b⊥c,则a∥b或a,b相交或a,b异面,故③错;
④若a⊥M,b⊥M,则a∥b,故④正确.
故选A.
②若b?M,a∥b,a?M,则a∥M,故②错;
③a⊥c,b⊥c,则a∥b或a,b相交或a,b异面,故③错;
④若a⊥M,b⊥M,则a∥b,故④正确.
故选A.
点评:本题主要考查空间直线与平面的位置关系:平行和垂直,考查线面平行与垂直的判定和性质,熟记这些是迅速解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知函数f(x)=(
)x-log2x,若实数x0是函数f(x)的零点,且0<x<x0,则函数f(x)的值( )
| 1 |
| 3 |
| A、等于0 | B、恒为正 |
| C、恒为负 | D、不大于0 |
已知盒中装有3只螺口与2只卡口灯泡,这些灯泡的外形与功率都相同且灯口向下放着,现需要一只卡口灯泡,电工师傅每次从中任取一只并不放回,则在他第1次抽到的是螺口灯泡的条件下,第2次抽到的是卡口灯泡的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若
与
不共线,实数x、y满足等式2x
+(3-y)
=x
+(3y+1)
,则实数x+y=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-2 |
两球的体积之比为8:1,则它们的表面积之比为( )
| A、8:1 | ||
| B、4:1 | ||
C、2
| ||
| D、2:1 |
执行如图所示的程序框图,若输出的k=6,则输入的整数p的最大值为( )
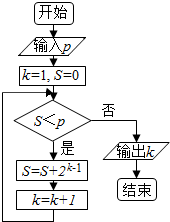

| A、7 | B、15 | C、31 | D、63 |
长方体的一个顶点上三条棱长分别是1、2、3,且它的8个顶点都在同一球面上,则这个球的表面积是( )
| A、7π | B、14π |
| C、28π | D、56π |