题目内容
已知在△ABC中,A为动点,B、C为定点,B(-
,0),C(
,0)(a>0)且满足条件|sinC-sinB|=
sinA,则动点A的轨迹方程是( )
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:轨迹方程,正弦定理
专题:计算题,圆锥曲线的定义、性质与方程
分析:由|sinC-sinB|=
sinA,得|c-b|=
a,可得动点A的轨迹为双曲线,且实轴长为
a,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由|sinC-sinB|=
sinA,得|c-b|=
a,∴动点A的轨迹为双曲线,且实轴长为
a,
∵B(-
,0),C(
,0)(a>0),
∴焦距为a,
故方程为
-
=1(y≠0).
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵B(-
| a |
| 2 |
| a |
| 2 |
∴焦距为a,
故方程为
| 16x2 |
| a2 |
| 16y2 |
| 15a2 |
故选:A.
点评:本题考查双曲线方程,考查学生的计算能力,确定动点A的轨迹为双曲线,且实轴长为
a是关键.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
x3+
x2+(a+b)x+c(a,b,c∈R)的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,+∞),z=2a-b,则z的取值范围是( )
| 1 |
| 3 |
| a |
| 2 |
| A、(-∞,3] |
| B、(-∞,-3) |
| C、[-3,+∞) |
| D、(-3,+∞) |
 如图,在四棱锥P-ABCD中,底面四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,则二面角P-CD-B的大小是
如图,在四棱锥P-ABCD中,底面四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,则二面角P-CD-B的大小是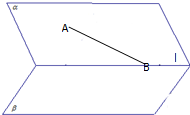 如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )
如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )