题目内容
2. 某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:
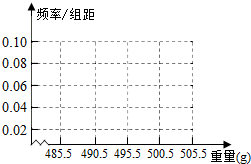
某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:(1)请补充完成频率分布表,并在下图中画出频率分布直方图;
(2)根据上述数据估计从这批白糖中随机抽取一袋其重量在[495.5,505.5]上的概率.
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | |
| [490.5,495.5) | 0.20 | |
| [495.5,500.5) | 50 | |
| [500.5,505.5] | ||
| 合计 | 100 |
分析 (1)由频率=$\frac{频数}{总数}$,能完成频率分布表,根据频率分布表,能画出频率分布直方图.
(2)由频率分布直方图能估计从这批白糖中随机抽取一袋其重量在[495.5,505.5]上的概率.
解答  (本题满分8分)
(本题满分8分)
解:(1)由频率=$\frac{频数}{总数}$,得[490.5,495.5)组中的频数为:100×0.2=20,
[500.5,505.5)组中的频数为:100-10-20-50=20,[500.5,505.5)组中的频率为:$\frac{20}{100}$=0.2.
由此完成频率分布表如下:
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | 0.10 |
| [490.5,495.5) | 20 | 0.20 |
| [495.5,500.5) | 50 | 0.50 |
| [500.5,505.5] | 20 | 0.20 |
| 合计 | 100 | 1.00 |
(2)由频率分布直方图估计从这批白糖中随机抽取一袋其重量在[495.5,505.5]上的概率:
p=(0.04+0.1)×5=0.7.
点评 本题考查频率分布表、频率分布直方图的作法,考查概率的求法,是基础题,解时要注意公式频率=$\frac{频数}{总数}$的合理运用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
10.在平面直角坐标系xOy中,圆M的方程为x2+y2-8x-2y+16=0,若直线kx-y+3=0上至少存在一点,使得以该点为圆心,半径为1的圆与圆M有公共点,则k的取值范围是( )
| A. | (-∞,$\frac{4}{3}$] | B. | [0,+∞) | C. | [-$\frac{4}{3}$,0] | D. | (-∞,$\frac{4}{3}$]∪[0,+∞) |
11.下列各式中,值为$\frac{1}{2}$的是( )
| A. | sin15°cos15° | B. | cos2$\frac{π}{12}$-sin2$\frac{π}{12}$ | ||
| C. | $\frac{tan22.5°}{1-ta{n}^{2}22.5°}$ | D. | $\frac{1+tan15°}{1-tan15°}$ |
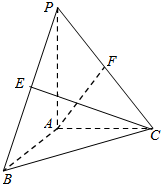 (理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
(理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.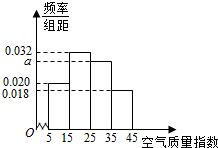 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.