题目内容
已知函数f(x)=|x+2|-|x-1|.
(Ⅰ)将f(x)写成分段函数的形式;
(Ⅱ)画出f(x)的图象.
(Ⅰ)将f(x)写成分段函数的形式;
(Ⅱ)画出f(x)的图象.
考点:分段函数的应用,函数的图象
专题:函数的性质及应用
分析:(Ⅰ)根据绝对值的几何意义即可将f(x)写成分段函数的形式;
(Ⅱ)利用分段函数的表达式,即可作出函数的图象.
(Ⅱ)利用分段函数的表达式,即可作出函数的图象.
解答:
解:(Ⅰ)当x<-2时,f(x)=|x+2|-|x-1|=-x-2+x-1=-3,
当-2≤x≤1时,f(x)=|x+2|-|x-1|=x+2+x-1=2x+1,
当x>1时,f(x)=|x+2|-|x-1|=x+2-x+1=3,
故f(x)=
.
(Ⅱ)作出函数的图象如图:

当-2≤x≤1时,f(x)=|x+2|-|x-1|=x+2+x-1=2x+1,
当x>1时,f(x)=|x+2|-|x-1|=x+2-x+1=3,
故f(x)=
|
(Ⅱ)作出函数的图象如图:

点评:本题主要考查分段函数的应用,根据绝对值的几何意义是解决本题的关键.

练习册系列答案
相关题目
设函数f(x)=x2─2,用二分法求f(x)=0的一个近似解时,第1步确定了一个区间为(1,
),到第3步时,求得的近似解所在的区间应该是( )
| 3 |
| 2 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
曲线y=
与直线x=1,x=e2及x轴所围成的图形的面积是( )
| 1 |
| x |
| A、e2 |
| B、e2-1 |
| C、e |
| D、2 |
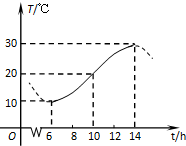 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中ω>0,
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中ω>0,| π |
| 2 |
| A、30℃ | B、27℃ |
| C、25℃ | D、24℃ |
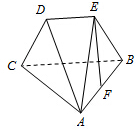 在多面体ABCDE中,BC=BA,DE∥BC,AE⊥平面BCDE,BC=2DE,F为AB的中点.
在多面体ABCDE中,BC=BA,DE∥BC,AE⊥平面BCDE,BC=2DE,F为AB的中点.