题目内容
函数y=
的图象和其在点(-1,1)处的切线与x轴所围成区域的面积为 .
| -x |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数y=
的导函数,得到函数在点(-1,1)处的切线方程,把函数y=
的图象和其在点(-1,1)处的切线与x轴所围成区域的面积转化为定积分求解.
| -x |
| -x |
解答:
解:由y=
,得y′=-
,
∴y′|x=-1=-
,
则函数y=
的图象在点(-1,1)处的切线方程为:y=-
(x+1)+1=-
x+
.
函数y=
的图象和其在点(-1,1)处的切线与x轴所围成区域的面积:
S=
(-
x+
-
)dx
(-
x+
)dx
=(-
x2+
x+
(-x)
)
+(-
x2+
x)
=
.
故答案为:
.
| -x |
| 1 | ||
2
|
∴y′|x=-1=-
| 1 |
| 2 |
则函数y=
| -x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
函数y=
| -x |
S=
| ∫ | 0 -1 |
| 1 |
| 2 |
| 1 |
| 2 |
| -x |
| +∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
=(-
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 0 -1 |
| 1 |
| 4 |
| 1 |
| 2 |
| | | 1 0 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查了导数的几何意义,曲线在点(x0,y0)处的切线斜率即为该点处的导数值,考查了定积分的几何意义,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点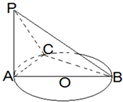 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )