题目内容

已知O为坐标原点，点A（2，0），动点P与两点O、A的距离之比为1：
3
，则P点轨迹方程是
 
．
考点：轨迹方程
专题：计算题,直线与圆
分析：设P（x，y），由已知条件利用两点间距离公式得（x-2）2+y2=3（x2+y2），由此能求出P点的轨迹方程．
解答： 解：设P（x，y），
∵动点P到两点O、A的距离之比为1：
3
，
∴|PA|=
3
|PO|，
∴（x-2）2+y2=3（x2+y2），
化简得（x+1）2+y2=3，
故答案为：（x+1）2+y2=3．
点评：本题考查点的轨迹方程的求法，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知圆C1：x2+y2+2x+6y+6=0，圆C2：x2+y2-4x-8y+7=0，求两圆的圆心距．
数列{an}满足a1=
π
6
，an∈（-
π
2
，
π
2
），且tanan+1•cosan=1（n∈N*）．
（Ⅰ）证明数列{tan2an}是等差数列，并求数列{tan2an}的前n项和；
（Ⅱ）求正整数m，使得11sina1•sina2•…•sinam=1．
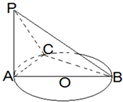如图，AB是圆O的直径，PA垂直圆O所在的平面，C是圆周上不同于A、B的任意一点，则图中直角三角形的个数为（　　）
A、1B、2C、3D、4
已知函数f（x）在（-1，1）上有定义，且f（
1
5
）=
1
2
．对任意x，y∈（-1，1）都有f（x）+f（y）=f（
x+y
1+xy
），当且仅当-1＜x＜0时，f（x）＞0．
（1）判断f（x）在（-1，1）上的奇偶性，并说明理由；
（2）判断f（x）在（0，1）上的单调性，并说明理由；
（3）试求f（
1
2
）-f（
1
11
）-f（
1
19
）的值．
已知函数f（x）=|x+2|-|x-1|．
（Ⅰ）将f（x）写成分段函数的形式；
（Ⅱ）画出f（x）的图象．
已知函数y=f（x），若在区间（-2，2）内有且仅有一个x0，使得f（x0）=1成立，则称函数f（x）具有性质M．
（Ⅰ）若f（x）=sinx+2，判断f（x）是否具有性质M，说明理由；
（Ⅱ）若函数f（x）=x2+2mx+2m+1具有性质M，试求实数m的取值范围．
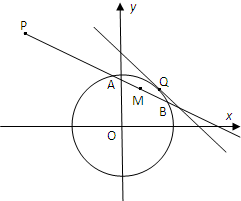过点P（-4，4）作直线l与圆O：x2+y2=4相交于A、B两点．
（Ⅰ）若直线l变动时，求AB中点M的轨迹方程；
（Ⅱ）若直线l的斜率为-
1
2
，求弦AB的长；
（Ⅲ）若一直线与圆O相 切于点Q且与x轴的正半轴，y轴的正半轴围成一个三角形，当该三角形面积最小时，求点Q的坐标．
已知a＞b，c＞d，则下列不等式成立的是（　　）
A、b+d＜a+c
B、ac＞bd
C、
a
c
＞
d
b
D、a-c＞b-d

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网