题目内容
某人向一目标射击,在A处射击一次击中目标的概率为0.2,击中目标得2分;在B处射击一次击中目标的概率为q,击中目标得1分.若他射击三次,第一次在A处射击,后两次都在B处射击,用ξ表示他3次射击后得的总分,其分布列为:
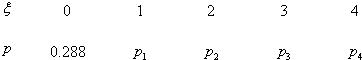
(1)求q及的数学期望Eξ;
(2)求此人3次都选择A处向目标射击且得分高于2分的概率.
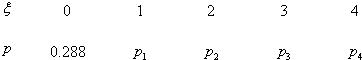
(1)求q及的数学期望Eξ;
(2)求此人3次都选择A处向目标射击且得分高于2分的概率.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)由(1-0.2)(1-q)2=0.288,能求出q及的数学期望Eξ.
(2)3次射击得分高于2分,就是3次射击至少有两次击中目标,由此能求出此人3次都选择A处向目标射击且得分高于2分的概率.
(2)3次射击得分高于2分,就是3次射击至少有两次击中目标,由此能求出此人3次都选择A处向目标射击且得分高于2分的概率.
解答:
解:(1)由(1-0.2)(1-q)2=0.288,得q=0.4,…(2分)
p1=0.8×
×0.4×0.6=0.384,
p2=0.2×0.62+0.8×0.42=0.2,
p3=0.2×
×0.4×0.6=0.096,
p4=0.2×0.42=0.032,…(8分)
Eξ=0.384×1+0.2×2+0.096×3+0.032×4=1.2.…(10分)
(2)∵3次射击得分高于2分,就是3次射击至少有两次击中目标,
∴所求概率为
×0.8×0.22+0.23=0.104.…(12分)
p1=0.8×
| C | 1 2 |
p2=0.2×0.62+0.8×0.42=0.2,
p3=0.2×
| C | 1 2 |
p4=0.2×0.42=0.032,…(8分)
Eξ=0.384×1+0.2×2+0.096×3+0.032×4=1.2.…(10分)
(2)∵3次射击得分高于2分,就是3次射击至少有两次击中目标,
∴所求概率为
| C | 1 2 |
点评:本题考查概率、随机变量分布列以及数学期望等基础知识,考查运用概率统计知识解决简单实际问题的能力,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
有一座七层塔,每层所点灯的盏数都是其上面一层的两倍,这座塔一共点381盏灯,则底层所点灯的盏数是( )
| A、190 | B、191 |
| C、192 | D、193 |
 以下茎叶图记录了甲、乙两组各5名同学在一次英语听力测试中的成绩(单位:分)
以下茎叶图记录了甲、乙两组各5名同学在一次英语听力测试中的成绩(单位:分)