题目内容
某校高一某班的一次数学周练成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
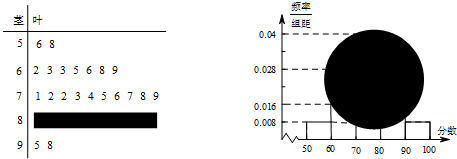
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)根据频率分布直方图估计全班数学成绩的平均分;
(Ⅲ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求恰好在
[80,90),[90,100]各取一份分数的概率.

(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)根据频率分布直方图估计全班数学成绩的平均分;
(Ⅲ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求恰好在
[80,90),[90,100]各取一份分数的概率.
考点:古典概型及其概率计算公式,频率分布直方图,茎叶图
专题:概率与统计
分析:(Ⅰ)求出分数在[50,60)的频率,分数在[50,60)之间的频数,即可求解全班人数.
(Ⅱ)全班人数共25人,根据各分数段人数计算得各分数段的频率,然后估计这次测试的平均成绩即可.
(Ⅲ)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,列出在[80,100]之间的试卷中任取两份的基本事件,恰好在[80,90),[90,100]各取一份分数的基本事件有8个,然后求解概率.
(Ⅱ)全班人数共25人,根据各分数段人数计算得各分数段的频率,然后估计这次测试的平均成绩即可.
(Ⅲ)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,列出在[80,100]之间的试卷中任取两份的基本事件,恰好在[80,90),[90,100]各取一份分数的基本事件有8个,然后求解概率.
解答:
解:(Ⅰ)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为
=25,
(Ⅱ)全班人数共25人,根据各分数段人数计算得各分数段的频率为:
所以估计这次测试的平均成绩为:55×0.08+65×0.28+75×0.4+85×0.16+95×0.08=73.8.
(Ⅲ)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.其中,恰好在[80,90),[90,100]各取一份分数的基本事件有8个,故概率是
.
| 2 |
| 0.08 |
(Ⅱ)全班人数共25人,根据各分数段人数计算得各分数段的频率为:
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频率 | 0.08 | 0.28 | 0.4 | 0.16 | 0.08 |
(Ⅲ)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.其中,恰好在[80,90),[90,100]各取一份分数的基本事件有8个,故概率是
| 8 |
| 15 |
点评:本题考查频率分布直方图,茎叶图以及古典概型计算公式的应用,基本知识的考查.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
在△ABC中,若acos2
+ccos2
=
b,那么a,b,c的关系是( )
| C |
| 2 |
| A |
| 2 |
| 3 |
| 2 |
| A、a+b=c |
| B、a+c=2b |
| C、b+c=2a |
| D、a=b=c |
为了了解全校200名学生视力的情况.从中抽取50名学生进行测量.下列说法正确的是( )
| A、总体是200 |
| B、个体是每名学生 |
| C、样本为50名学生 |
| D、样本容量为50 |
满足条件M∪{1}={1,2,3}的集合M的个数是( )
| A、1 | B、2 | C、3 | D、4 |