题目内容
若底边长为2的正四棱锥内切一半径为
的球,则此正四棱锥的体积是 .
| 1 |
| 2 |
考点:球内接多面体,棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离,球
分析:运用分割思想,连接OP,OA,OB,OC,OD,得到四个三棱锥和一个四棱锥,由大的四棱锥的体积等于四个三棱锥的体积和一个小的四棱锥的体积之和,根据正四棱锥的性质,求出斜高,即可求出正四棱锥的高,从而得到正四棱锥的体积.
解答:
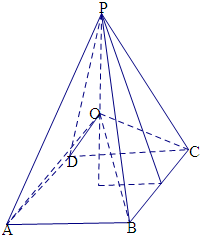 解:设正四棱锥的高为h,连接OP,OA,OB,OC,OD,
解:设正四棱锥的高为h,连接OP,OA,OB,OC,OD,
得到四个三棱锥和一个四棱锥,它们的高均为
,
则VP-ABCD=VO-PAB+VO-PAD+VO-PBC+VO-PCD+VO-ABCD
即
h×22=
×
(4×S△PBC+4),
由四棱锥的高和斜高,及斜高在底面的射影构成的直角三角形得到,
斜高为
,
∴S△PBC=
×2
=
,
∴2h=1+
,解得,h=
.
则正四棱锥的体积为
×4×
=
.
故答案为:
.
 解:设正四棱锥的高为h,连接OP,OA,OB,OC,OD,
解:设正四棱锥的高为h,连接OP,OA,OB,OC,OD,得到四个三棱锥和一个四棱锥,它们的高均为
| 1 |
| 2 |
则VP-ABCD=VO-PAB+VO-PAD+VO-PBC+VO-PCD+VO-ABCD
即
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
由四棱锥的高和斜高,及斜高在底面的射影构成的直角三角形得到,
斜高为
| h2+1 |
∴S△PBC=
| 1 |
| 2 |
| h2+1 |
| h2+1 |
∴2h=1+
| h2+1 |
| 4 |
| 3 |
则正四棱锥的体积为
| 1 |
| 3 |
| 4 |
| 3 |
| 16 |
| 9 |
故答案为:
| 16 |
| 9 |
点评:本题主要考查球与正四棱锥的关系,通过分割,运用体积转换的思想,是解决本题的关键.

练习册系列答案
相关题目
已知等比数列{an}的公比为q,且a1>0,则“q>0”是“数列{an}为递增数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
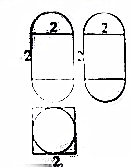 某几何体的三视图如图所示,则该几何体的体积( )
某几何体的三视图如图所示,则该几何体的体积( )A、4+
| ||
B、8+
| ||
C、8+
| ||
D、8+
|
已知圆O:x2+y2=1,直线l:3x+4y-3=0,则直线l被圆O所截的弦长为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
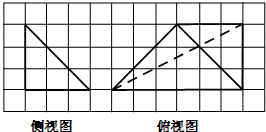 如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )