题目内容
7.雾霾天气对人体健康有害,应对雾霾污染、改善空气质量是当前的首要任务是控制PM2.5,要从压减燃煤、严格控产、调整产业、强化管理、联防联控、依法治理等方面采取重大举措,聚焦重点领域,严格考核指标.某省环保部门为加强环境执法监管,派遣四个不同的专家组对A,B,C三个城市进行雾霾落实情况抽查.(1)若每个专家组随机选取一个城市,四个专家组选取的城市可以相同,也可以不同,且每个城市都必须由专家组选取,求A城市恰有两有专家组选取的概率;
(2)在检查的过程中专家组从A城市的居民中随机抽取出400人进行是否户外作业人员与是否患有呼吸道疾病进行了统计,统计结果如下:
| 分类 | 患呼吸道疾病 | 未患呼吸道疾病 | 合计 |
| 户外作业人员 | 40 | 60 | 100 |
| 非户外作业人员 | 60 | 240 | 300 |
| 合计 | 100 | 300 | 400 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)确定基本事件的情况,即可求出相应的概率;
(2)求出K2,与临界值比较,即可得出结论.
解答 解:(1)∵四个专家组选取的城市可以相同,也可以不同,且每个城市都必须由专家组选取,
∴不同的选取方法有${C}_{3}^{1}{C}_{4}^{2}{A}_{2}^{2}$=36种方法,
A城市恰有两名专家组选取方法有12种,故概率为$\frac{1}{3}$;
(2)K2=$\frac{400(40×240-60×60)^{2}}{100×300×100×300}$=16>6.635,
∴有超过99%的把握认为“户外作业”与“患有呼吸道疾病”有关.
点评 本题考查概率的计算,考查独立性检验知识的运用,正确计算是关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.△ABC的内角A,B,C的对边分别是a,b,c,若B=2A,a=1,b=$\sqrt{3}$,则角B=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
19.双曲线$\frac{y^2}{3}-\frac{x^2}{6}=1$的一个焦点坐标为( )
| A. | (3,0) | B. | (0,3) | C. | $(\sqrt{3},0)$ | D. | $(0,\sqrt{3})$ |
16.某农场所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了2017年2月1日至2月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表:
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的两组数据进行检验.
(Ⅰ)求选取的2组数据恰好是不相邻的2天数据的概率;
(Ⅱ)若选取的是2月1日与2月5日的两组数据,请根据2月2日至2月4日的数据,求出y关于x的线性回归方程
$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;可以预报当温差为20℃时,种子发芽数.
附:回归直线方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$;$\stackrel{∧}{b}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数x(颗) | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)求选取的2组数据恰好是不相邻的2天数据的概率;
(Ⅱ)若选取的是2月1日与2月5日的两组数据,请根据2月2日至2月4日的数据,求出y关于x的线性回归方程
$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;可以预报当温差为20℃时,种子发芽数.
附:回归直线方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$;$\stackrel{∧}{b}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
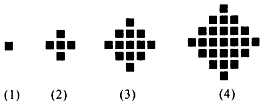 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.