题目内容
17．
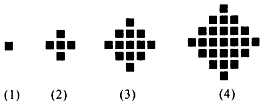某民族的刺绣有着悠久的历史，如图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．先按照同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．（1）求出f（6）的值；
（2）利用合情推理的“归纳推理思想”归纳出f（n+1）与f（n）之间的关系式，并根据你得到的关系式求出f（n）的表达式．
分析 （1）根据题意，写出f（1）、f（2）、f（3）、f（4）和f（5），f（6）的值；
（2）根据前面5个函数值，得出规律，f（n）-f（n-1）=4（n-1），从而求出f（n）的表达式．
解答 解：（1）根据题意，得出
f（1）=1，f（2）=5，
f（3）=13，f（4）=25，
f（5）=41，f（6）=61；
（2）根据前面四个发现规律：
f（2）-f（1）=4×1，
f（3）-f（2）=4×2，
f（4）-f（3）=4×3，
…，
f（n）-f（n-1）=4（n-1）；
这n-1个式子相加可得：f（n）=2n2-2n+1．
点评 本题考查了归纳推理的应用问题，基本思路是先分析，观察，总结其内在联系，得到一般性的结论，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．雾霾天气对人体健康有害，应对雾霾污染、改善空气质量是当前的首要任务是控制PM2.5，要从压减燃煤、严格控产、调整产业、强化管理、联防联控、依法治理等方面采取重大举措，聚焦重点领域，严格考核指标．某省环保部门为加强环境执法监管，派遣四个不同的专家组对A，B，C三个城市进行雾霾落实情况抽查．
（1）若每个专家组随机选取一个城市，四个专家组选取的城市可以相同，也可以不同，且每个城市都必须由专家组选取，求A城市恰有两有专家组选取的概率；
（2）在检查的过程中专家组从A城市的居民中随机抽取出400人进行是否户外作业人员与是否患有呼吸道疾病进行了统计，统计结果如下：
根据上述的统计结果，我们是否有超过99%的把握认为“户外作业”与“患有呼吸道疾病”有关？
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
（1）若每个专家组随机选取一个城市，四个专家组选取的城市可以相同，也可以不同，且每个城市都必须由专家组选取，求A城市恰有两有专家组选取的概率；
（2）在检查的过程中专家组从A城市的居民中随机抽取出400人进行是否户外作业人员与是否患有呼吸道疾病进行了统计，统计结果如下：
| 分类 | 患呼吸道疾病 | 未患呼吸道疾病 | 合计 |
| 户外作业人员 | 40 | 60 | 100 |
| 非户外作业人员 | 60 | 240 | 300 |
| 合计 | 100 | 300 | 400 |
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12．已知函数f（x）=$\left\{\begin{array}{l}{e^x}，x≥0\\ ax，x＜0\end{array}$若方程f（-x）=f（x）有五个不同的实根，则实数a的取值范围（ ）
| A． | （1，+∞） | B． | （e，+∞） | C． | （-∞，-1） | D． | （-∞，-e） |
2．已知$cos（\frac{π}{6}+x）=\frac{1}{3}$，则$cos（\frac{5π}{6}-x）$的值为（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $-\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
6．用分析法证明：欲证①A＞B，只需证②C＜D，这里②是①的（ ）
| A． | 充分条件 | B． | 必要条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
7．cos$（\frac{-13π}{4}）$的值为（ ）
| A． | $-\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |