题目内容
三角形两边之差为2,夹角的正弦值为
,面积为
,那么这个三角形的两边长分别是 .
| 3 |
| 5 |
| 9 |
| 2 |
考点:解三角形
专题:计算题,解三角形
分析:利用面积公式得出ac的值,与a-c=2联立即可得出a,c的值.
解答:
解:如图所示, 已知a-c=2,sinB=
已知a-c=2,sinB=
,S△ABC=
.
∴
=
acsinB,∴ac=15,
∴a=5,c=3.
故答案为:5和3.
 已知a-c=2,sinB=
已知a-c=2,sinB=| 3 |
| 5 |
| 9 |
| 2 |
∴
| 9 |
| 2 |
| 1 |
| 2 |
∴a=5,c=3.
故答案为:5和3.
点评:本题考查三角形的面积公式,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
若正三棱柱ABC-A1B1C1的所有棱长都相等,则AC1和平面BB1C1C所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、C
| ||||
D、
|
下列有关命题的说法正确的是( )
| A、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
| B、“x=1”是“x2-5x-6=0”的必要而不充分的条件 |
| C、命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” |
| D、命题“若x=y则sinx=siny”的逆否命题为真命题 |
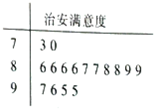 某网站用“10分制”调查一社区人们的治安满意度,现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某网站用“10分制”调查一社区人们的治安满意度,现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):