题目内容
如图所示,某几何体的三视图在网格纸上,且网格纸上小正方形的边长为1,则该几何体的体积为( )


| A、6π+4 |
| B、12π+4 |
| C、6π+12 |
| D、12π+12 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:先由三视图判断出几何体的形状及度量长度,然后利用三棱锥的体积公式及柱体的体积公式求解.
解答:
解:由已知中的三视图可得该几何体是一个半圆柱与三棱锥的组合体,
半圆柱的半径为2,高为3,故体积为:
×π×22×3=6π,
三棱锥的底面两直角边长为2和4,高为3,故体积为:
×
×2×4×3=4,
故组合体的体积V=6π+4,
故选:A
半圆柱的半径为2,高为3,故体积为:
| 1 |
| 2 |
三棱锥的底面两直角边长为2和4,高为3,故体积为:
| 1 |
| 3 |
| 1 |
| 2 |
故组合体的体积V=6π+4,
故选:A
点评:解决三视图的题目,关键是由三视图判断出几何体的形状及度量长度,然后利用几何体的面积及体积公式解决.

练习册系列答案
相关题目
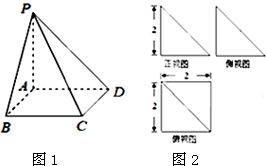 已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.
已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.(Ⅰ)求此四棱锥的体积;
(Ⅱ)求证:PB∥平面ACE;
(Ⅲ)求证:AE⊥PC.
数列{an}中,a1=a2=1,an+2=an+1+an对所有正整数n都成立,则a10等于( )
| A、34 | B、55 | C、89 | D、100 |



