题目内容
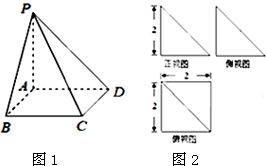 已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.
已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.(Ⅰ)求此四棱锥的体积;
(Ⅱ)求证:PB∥平面ACE;
(Ⅲ)求证:AE⊥PC.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:证明题,空间位置关系与距离
分析:(Ⅰ)先求底面面积,由棱锥的体积公式即可求值;
(Ⅱ)先证明EO∥PB,又由EO?平面ACE,PB?平面ACE,即可证明PB∥平面ACE;
(Ⅲ)先证明CD⊥AD,再证明AE⊥CD,有AE⊥PD,从而可证AE⊥平面PCD,由PC?平面PCD,从而可证AE⊥PC.
(Ⅱ)先证明EO∥PB,又由EO?平面ACE,PB?平面ACE,即可证明PB∥平面ACE;
(Ⅲ)先证明CD⊥AD,再证明AE⊥CD,有AE⊥PD,从而可证AE⊥平面PCD,由PC?平面PCD,从而可证AE⊥PC.
解答:
解:(Ⅰ)由题意可知四棱锥P-ABCD的底面是边长为2的正方形,其面积SABCD=2×2=4,高h=2,
所以VP-ABCD=
×4×2=
,(4分)
(Ⅱ)由三视图可知,ABCD是正方形,连接AC、BD交于点O,则O是BD的中点,又E是PD的中点,
所以EO是三角形PBD的中位线,
所以EO∥PB,又EO?平面ACE,
PB?平面ACE,所以PB∥平面ACE; (8分)
(Ⅲ)由三视图可知,PA⊥平面ABCD,∴CD⊥PA (9分)
∵ABCD是正方形,∴CD⊥AD (10分)
又∵PA∩AD=A,PA?平面ABCD,AD?平面ABCD
∴CD⊥平面PAD,∵AE?平面PAD,∴AE⊥CD (12分)
又∵△PAD是等腰直角三角形,E为PD的中点,∴AE⊥PD
又∵PD∩CD=D,PD?平面PCD,CD?平面PCD
∴AE⊥平面PCD,(13分)
又∵PC?平面PCD
∴AE⊥PC (14分)
所以VP-ABCD=
| 1 |
| 3 |
| 8 |
| 3 |
(Ⅱ)由三视图可知,ABCD是正方形,连接AC、BD交于点O,则O是BD的中点,又E是PD的中点,
所以EO是三角形PBD的中位线,
所以EO∥PB,又EO?平面ACE,
PB?平面ACE,所以PB∥平面ACE; (8分)
(Ⅲ)由三视图可知,PA⊥平面ABCD,∴CD⊥PA (9分)
∵ABCD是正方形,∴CD⊥AD (10分)
又∵PA∩AD=A,PA?平面ABCD,AD?平面ABCD
∴CD⊥平面PAD,∵AE?平面PAD,∴AE⊥CD (12分)
又∵△PAD是等腰直角三角形,E为PD的中点,∴AE⊥PD
又∵PD∩CD=D,PD?平面PCD,CD?平面PCD
∴AE⊥平面PCD,(13分)
又∵PC?平面PCD
∴AE⊥PC (14分)
点评:本题主要考察了直线与平面平行的判定,棱柱、棱锥、棱台的体积公式的应用,属于基本知识的考查.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
如图所示,某几何体的三视图在网格纸上,且网格纸上小正方形的边长为1,则该几何体的体积为( )


| A、6π+4 |
| B、12π+4 |
| C、6π+12 |
| D、12π+12 |
 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,AB=AC,D,E分别为BC,BB1的中点,四边形B1BCC1是正方形.
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,AB=AC,D,E分别为BC,BB1的中点,四边形B1BCC1是正方形.