题目内容
数列{an}中，a1=a2=1，an+2=an+1+an对所有正整数n都成立，则a10等于（ ）
| A、34 | B、55 | C、89 | D、100 |
考点：数列递推式
专题：等差数列与等比数列
分析：由已知条件利用递推思想求解．
解答：
解：∵数列{an}中，a1=a2=1，
an+2=an+1+an对所有正整数n都成立，
∴a3=1+1=2，
a4=2+1=3，
a5=3+2=5，
a6=5+3=8，
a7=8+5=13，
a8=13+8=21，
a9=21+13=34，
a10=34+21=55．
故选：B．
an+2=an+1+an对所有正整数n都成立，
∴a3=1+1=2，
a4=2+1=3，
a5=3+2=5，
a6=5+3=8，
a7=8+5=13，
a8=13+8=21，
a9=21+13=34，
a10=34+21=55．
故选：B．
点评：本题考查数列的第10项的求法，解题时要认真审题，注意递推公式的合理运用．
练习册系列答案
相关题目
如图所示，某几何体的三视图在网格纸上，且网格纸上小正方形的边长为1，则该几何体的体积为（ ）
| A、6π+4 |
| B、12π+4 |
| C、6π+12 |
| D、12π+12 |
若数列{an}的前n项和为Sn对任意正整数n都有Sn=2an-1，则S6=（ ）
| A、32 | B、31 | C、64 | D、63 |
已知a、b为正实数，直线y=x-a与曲线y=ln（x+b）相切，则
的取值范围是（ ）
| a2 |
| 2+b |
A、（0，
| ||
| B、（0，1） | ||
| C、（0，+∞） | ||
| D、[1，+∞） |
如图，在三棱柱ABC-A1B1C1中，BB1⊥平面ABC，AB=AC，D，E分别为BC，BB1的中点，四边形B1BCC1是正方形．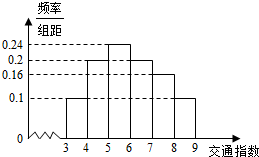
交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别：T∈[0，2）畅通；T∈[2，4）基本畅通；T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从贵阳市交通指挥中心随机选取了二环以内50个交通路段，依据交通指数数据绘制的直方图如图所示：