题目内容
已知函数f(x)=
,x∈[1,+∞),若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
| x2+x+a |
| x |
考点:函数恒成立问题
专题:转化思想,函数的性质及应用
分析:可将条件转化为:对任意x∈[1,+∞),x2+x+a>0恒成立,构造二次函数,注意对称轴与区间的关系,运用函数的单调性求出最小值,即可得到实数a的取值范围.
解答:
解:函数f(x)=
,且对任意x∈[1,+∞),f(x)>0恒成立,
即对任意x∈[1,+∞),x2+x+a>0恒成立,
令g(x)=x2+x+a,x∈[1,+∞),
则对任意x∈[1,+∞),g(x)min>0,
∵g(x)图象的对称轴为x=-
,
∴[1,+∞)为增区间,
∴g(1)为最小值且为2+a,
∴2+a>0即a>-2.
∴实数a的取值范围为:(-2,+∞).
| x2+x+a |
| x |
即对任意x∈[1,+∞),x2+x+a>0恒成立,
令g(x)=x2+x+a,x∈[1,+∞),
则对任意x∈[1,+∞),g(x)min>0,
∵g(x)图象的对称轴为x=-
| 1 |
| 2 |
∴[1,+∞)为增区间,
∴g(1)为最小值且为2+a,
∴2+a>0即a>-2.
∴实数a的取值范围为:(-2,+∞).
点评:本题考查函数恒成立问题可通过转化为求函数的最值来解决,可通过函数的单调性求出最值,注意掌握这种方法.

练习册系列答案
相关题目
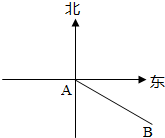 已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.