题目内容
已知数列{an}满足a1=2,a2=1,且
=
(n≥2).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=
anan+2,记数列{bn}的前n项和为Sn,试求使Sn<m-
恒成立的m的最小值.
| an+1 |
| an+1-an |
| an-1 |
| an-an-1 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=
| 1 |
| 2 |
| 1 |
| 2 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(I)由
=
(n≥2)变形为
+
=
.利用等差数列的通项公式即可得出.
(II)bn=
anan+2=
-
.利用“裂项求和”与数列的单调性即可得出.
| an+1 |
| an+1-an |
| an-1 |
| an-an-1 |
| 1 |
| an+1 |
| 1 |
| an-1 |
| 2 |
| an |
(II)bn=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
解答:
解:(I)由
=
(n≥2).化为
+
=
.
∴数列{
}是等差数列,
=
,公差的=
-
=1-
=
.
∴
=
+(n-1)×
=
.
∴an=
.
(II)bn=
anan+2=
×
×
=
-
.
∴数列{bn}的前n项和为Sn=(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)
=1+
-
-
≤1+
-
-
=
.
∵Sn≤m-
恒成立,
∴
≤m-
,
化为m≥
.
∴m的最小值是
.
| an+1 |
| an+1-an |
| an-1 |
| an-an-1 |
| 1 |
| an+1 |
| 1 |
| an-1 |
| 2 |
| an |
∴数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∴an=
| 2 |
| n |
(II)bn=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| n |
| 2 |
| n+2 |
| 1 |
| n |
| 1 |
| n+2 |
∴数列{bn}的前n项和为Sn=(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=1+
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
∵Sn≤m-
| 1 |
| 2 |
∴
| 2 |
| 3 |
| 1 |
| 2 |
化为m≥
| 7 |
| 6 |
∴m的最小值是
| 7 |
| 6 |
点评:本题考查了等差数列的通项公式、“裂项求和”、恒成立问题等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列函数中,不具有奇偶性的是( )
| A、y=x2-1 | ||||
| B、y=sinxcosx | ||||
C、y=
| ||||
| D、y=lgx2 |
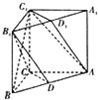 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.