题目内容
已知α为第一象限角，且sin2α+sinαcosα=
，tan（α-β）=-
，则tan（β-2α）的值为 ．
| 3 |
| 5 |
| 3 |
| 2 |
考点：两角和与差的正切函数
专题：三角函数的求值
分析：依题意，要求tan（β-2α）的值，需求得tanα的值，从而在条件“sin2α+sinαcosα=
”上动脑筋，想办法，“弦”化“切”即可．
| 3 |
| 5 |
解答：
解：∵sin2α+sinαcosα=
=
=
，
∴2tan2α+5tanα-3=0，又α为第一象限角，
解得：tanα=
，又tan（α-β）=-
，
∴tan（β-α）=
，
∴tan（β-2α）=tan[（β-α）-α]=
=
=
．
故答案为：
．
| sin2α+sinαcosα |
| sin2α+cos2α |
| tan2α+tanα |
| tan2α+1 |
| 3 |
| 5 |
∴2tan2α+5tanα-3=0，又α为第一象限角，
解得：tanα=
| 1 |
| 2 |
| 3 |
| 2 |
∴tan（β-α）=
| 3 |
| 2 |
∴tan（β-2α）=tan[（β-α）-α]=
| tan(β-α)-tanα |
| 1+tan(β-α)tanα |
| ||||
1+
|
| 4 |
| 7 |
故答案为：
| 4 |
| 7 |
点评：本题考查两角和与差的正切函数，求得tanα=
是关键，考查转化思想与观察、分析与运算能力，属于中档题．
| 1 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
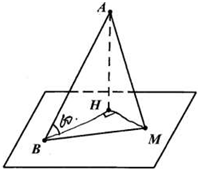某风景区有空中景点A及平坦的地面上景点B．已知AB与地面所成角的大小为60°，点A在地面上的射影为H，如图，请在地面上选定点M，使得