题目内容
已知函数f(x)=
-1(a>0)的图象在x=1处的切线为l,求l与两坐标轴围成的三角形面积的最小值.
| x2 |
| a |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数的导数,求出切线的斜率,切点坐标,求出切线方程,表示出三角形的面积利用基本不等式求出最值.
解答:
解:∵f′(x)=
,∴f′(1)=
.
又f(1)=
-1,切线的斜率为:
,切点坐标(1,
-1).
∴f(x)在x=1处的切线l的方程是y-
+1=
(x-1).
∴l与坐标轴围成的三角形的面积为
S=
|-
-1||
|=
(a+
+2)≥
×(2+2)=1.当且仅当a=1时等号成立.
l与两坐标轴围成的三角形面积的最小值为:1.
| 2x |
| a |
| 2 |
| a |
又f(1)=
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
∴f(x)在x=1处的切线l的方程是y-
| 1 |
| a |
| 2 |
| a |
∴l与坐标轴围成的三角形的面积为
S=
| 1 |
| 2 |
| 1 |
| a |
| a+1 |
| 2 |
| 1 |
| 4 |
| 1 |
| a |
| 1 |
| 4 |
l与两坐标轴围成的三角形面积的最小值为:1.
点评:本题考查函数的导数的应用,切线方程的求法,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
方程(
)x+x-3=0的解的个数有( )
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
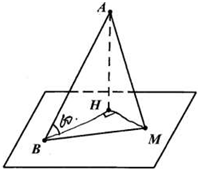 某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得
某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得