题目内容
已知函数f(x)=x2-6x+8,x∈[1,a],且函数f(x)的最小值为g(a),求g(a).
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先把函数的一般式变为顶点式,求出对称轴的方程,然后对不定区间进行具体的分类讨论,进一步求的结果.
解答:
解:函数f(x)=x2-6x+8=(x-3)2-1
函数是开口方向向上,对称轴方程为x=3的抛物线.
①当1<a<3时,g(a)=a2-6a+8;
②3≤a时,g(a)=-1.
故答案为:①当1<a<3时,g(a)=a2-6a+8;
②3≤a时,g(a)=-1.
函数是开口方向向上,对称轴方程为x=3的抛物线.
①当1<a<3时,g(a)=a2-6a+8;
②3≤a时,g(a)=-1.
故答案为:①当1<a<3时,g(a)=a2-6a+8;
②3≤a时,g(a)=-1.
点评:本题考查的知识点:二次函数一般式与顶点式的转换,对称轴方程和不定区间的讨论最后求出最小值.

练习册系列答案
相关题目
已知函数f(x)=x2+
,则“0<a<8”是“函数f(x)在(2,+∞)上为增函数”的( )
| a |
| x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
执行如图所示的程序框图,如果输出的p是720,那么输入的整数N是( )


| A、5 | B、6 | C、7 | D、8 |
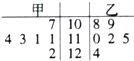 某质检机构检测某产品的质量是否合格,在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品,称其质量(单位:克),分别记录抽查数据,获得质量数据茎叶图(如图).
某质检机构检测某产品的质量是否合格,在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品,称其质量(单位:克),分别记录抽查数据,获得质量数据茎叶图(如图).