题目内容
从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛，若其中甲、乙两名同学不能参加生物竞赛，则选派方案共有（ ）
| A、180种 | B、280种 |
| C、96种 | D、240种 |
考点：计数原理的应用
专题：排列组合
分析：由题意知甲、乙两名同学不能参加生物竞赛，可以分不选甲乙，同时选甲乙，或选甲乙中的一个，根据分类计数原理可得，
解答：
解：由题意知甲、乙两名同学不能参加生物竞赛，可以分不选甲乙，同时选甲乙，或选甲乙中的一个，
第一类，不选甲乙时，有
=24种，
第二类，同时选甲乙时，甲乙只能从数学、物理、化学选2课，剩下的2课再从剩下的4人选2人即可，有
•
=72种，
第三类，选甲乙的一个时，甲或乙只能从数学、物理、化学选1课，剩下的3课再从剩下的4人选3人即可，有2
•
=144种，
根据分类计数原理得，24+72+144=240．
故选：D．
第一类，不选甲乙时，有
| A | 4 4 |
第二类，同时选甲乙时，甲乙只能从数学、物理、化学选2课，剩下的2课再从剩下的4人选2人即可，有
| A | 2 3 |
| A | 2 4 |
第三类，选甲乙的一个时，甲或乙只能从数学、物理、化学选1课，剩下的3课再从剩下的4人选3人即可，有2
| A | 1 3 |
| A | 3 4 |
根据分类计数原理得，24+72+144=240．
故选：D．
点评：本题主要考查分类计数原理，如何分类是关键，属于中档题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
已知向量
=（3，-1，2），
=（x，y，-4），且
∥
，则x+y=（ ）
| a |
| b |
| a |
| b |
| A、8 | B、4 | C、-4 | D、-8 |
已知向量
=（1，2），
=（3，1），则
+
=（ ）
| a |
| b |
| a |
| b |
| A、（-2，1） |
| B、（4，3） |
| C、（2，0） |
| D、（3，2） |
执行图示的程序框图，如果输入的x∈[-2，2]，则输出的y属于（ ）
A、[
| ||
B、（
| ||
C、[
| ||
D、（
|
已知P为抛物线y2=4x上一动点，则点P到y轴的距离与到点A（2，3）的距离之和的最小值为（ ）
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
如图，矩形ABCD所在的平面和平面ABEF互相垂直，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，∠BAF=60°，O，P分别为AB，CB的中点，M为底面△OBF的重心．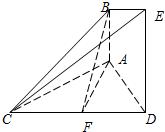
如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．