题目内容
某发射装置上有一个特殊的按键,在发射装置的屏幕上显示正整数n时按下这个键,会等可能的将其替换为0~n-1中的任意一个数,反复按这个键使得最终显示0,我们把这一操作称为“还原”操作.
(Ⅰ)设初始值为15,求在“还原”操作中出现9的概率;
(Ⅱ)当初始值为4时,进行“还原”操作,记操作次数为ξ,求ξ的概率分布列与数学期望.
(Ⅰ)设初始值为15,求在“还原”操作中出现9的概率;
(Ⅱ)当初始值为4时,进行“还原”操作,记操作次数为ξ,求ξ的概率分布列与数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由题意知对于数字n,对于任意一个不小于n+1的数,直接选择n的概率为
,直接选择n-1的概率为
,…,直接选择0的概率为
,而最后都选择了0,即概率和为1,所以数字n的出现概率即
.由此能求出在“还原”操作中出现9的概率.
(Ⅱ)由题意知ξ=1,2,3,4,分别求出相应的概率,由此能求出ξ的概率分布列和数学期望.
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
(Ⅱ)由题意知ξ=1,2,3,4,分别求出相应的概率,由此能求出ξ的概率分布列和数学期望.
解答:
解:(Ⅰ)由题意知:0出现的概率是1;
1出现的概率是
,因为对于任意不小于2的数,
直接选择1和选择0的概率是相同的,而选择了1就必然选择0,
所以选1再选零和直接选0概率相同;
对于数字n,对于任意一个不小于n+1的数,直接选择n的概率为
,
直接选择n-1的概率为
,…,直接选择0的概率为
,
而最后都选择了0,即概率和为1,所以数字n的出现概率即
.
∴在“还原”操作中出现9的概率p=
.
(Ⅱ)由题意知ξ=1,2,3,4,
P(ξ=1)=
,P(ξ=2)=
×
=
,P(ξ=3)=
×
×
=
,
P(ξ=4)=
×
×
×1=
,
∴ξ的概率分布列为:
Eξ=(1+2+3+4)×
=
.
1出现的概率是
| 1 |
| 2 |
直接选择1和选择0的概率是相同的,而选择了1就必然选择0,
所以选1再选零和直接选0概率相同;
对于数字n,对于任意一个不小于n+1的数,直接选择n的概率为
| 1 |
| n+1 |
直接选择n-1的概率为
| 1 |
| n+1 |
| 1 |
| n+1 |
而最后都选择了0,即概率和为1,所以数字n的出现概率即
| 1 |
| n+1 |
∴在“还原”操作中出现9的概率p=
| 1 |
| 10 |
(Ⅱ)由题意知ξ=1,2,3,4,
P(ξ=1)=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=4)=
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
∴ξ的概率分布列为:
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 5 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )
| A、180种 | B、280种 |
| C、96种 | D、240种 |
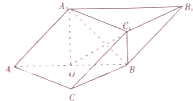 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.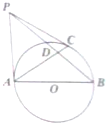 如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.
如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.