题目内容
已知两平面的法向量分别为
=(0,1,0),
=(0,1,1),则两平面所成的二面角为 .
| m |
| n |
考点:用空间向量求平面间的夹角
专题:计算题,空间角
分析:根据已知中两个平面法向量的夹角,代入向量夹角公式,可以求出两个向量的夹角,进而根据两平面所成的二面角与<
,
>相等或互补,得到答案.
| m |
| n |
解答:
解:∵两平面的法向量分别为
=(0,1,0),
=(0,1,1),
则两平面所成的二面角与<
,
>相等或互补
∵cos<
,
>=
=
故<
,
>=45°
故两平面所成的二面角为45°或135°.
故答案为:45°或135°.
| m |
| n |
则两平面所成的二面角与<
| m |
| n |
∵cos<
| m |
| n |
| 1 | ||
1•
|
| ||
| 2 |
故<
| m |
| n |
故两平面所成的二面角为45°或135°.
故答案为:45°或135°.
点评:本题考查的知识点是二面角的平面角及求法,其中一定要注意两平面所成的二面角与<
,
>相等或互补.
| m |
| n |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
函数y=xln|x|的大致图象是( )
A、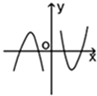 |
B、 |
C、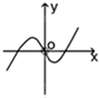 |
D、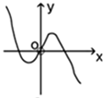 |
关于函数f(x)=sin(2x+
)的四个命题:
①f(x)的图象关于直线x=
对称;
②f(x)的图象关于点(
,0)对称;
③f(x)的最小正周期为π;
④f(x)在[0,
],上为增函数,其中正确的是命题是( )
| π |
| 3 |
①f(x)的图象关于直线x=
| π |
| 12 |
②f(x)的图象关于点(
| π |
| 4 |
③f(x)的最小正周期为π;
④f(x)在[0,
| π |
| 2 |
| A、②③ | B、①② | C、②④ | D、①③ |
在△ABC中,角A、B、C所对的边分别为a,b,c,且a>b,则正确的是( )
| A、sinA>sinB且cosA>cosB |
| B、sinA<sinB且cosA<cosB |
| C、sinA>sinB且cosA<cosB |
| D、sinA<sinB且cosA>cosB |