题目内容
四棱锥P-ABCD的所有侧棱长都为
，底面ABCD是边长为2的正方形，则CD与PA所成角的余弦值为 ．
| 5 |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：由AB∥CD，得到CD与PA所成的角为∠PAB，由此能求出CD与PA所成角的余弦值．
解答：
解：∵底面ABCD为正方形，
∴AB∥CD，
∴CD与PA所成的角为∠PAB，
∵AB=2，PA=PB=
，
∴cos∠PAB=
=
=
．
∴CD与PA所成角的余弦值为
．
故答案为：
．
∴AB∥CD，
∴CD与PA所成的角为∠PAB，
∵AB=2，PA=PB=
| 5 |
∴cos∠PAB=
| AB2+AP2-PA2 |
| 2AB•AP |
=
| 4+5-5 | ||
2×2×
|
=
| ||
| 5 |
∴CD与PA所成角的余弦值为
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查异面直线所成角的余弦值的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
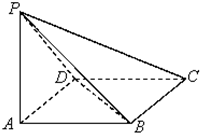如图，已知四棱锥P-ABCD，侧棱PA⊥平面ABCD，底面ABCD为菱形，∠DAB=60°且PA=AB，则直线AB与平面PBC所成角的正弦值为
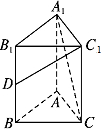如图，直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，∠B1A1C1=90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上是增函数．令a=f（sin
），b=f（cos
），c=f（tan
），则（ ）
| 5π |
| 7 |
| 2π |
| 7 |
| 2π |
| 7 |
| A、b＜a＜c |
| B、c＜b＜a |
| C、b＜c＜a |
| D、a＜b＜c |