题目内容
函数y=xln|x|的大致图象是( )
A、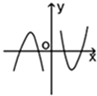 |
B、 |
C、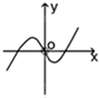 |
D、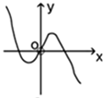 |
考点:函数的图象
专题:函数的性质及应用
分析:容易看出,该函数是奇函数,所以排除B项,再原函数式化简,去掉绝对值符号转化为分段函数,再从研究x>0时,特殊的函数值符号、极值点、单调性、零点等性质进行判断.
解答:
解:令f(x)=xln|x|,易知f(-x)=-xln|-x|=-xln|x|=-f(x),所以该函数是奇函数,排除选项B;
又x>0时,f(x)=xlnx,容易判断,当x→+∞时,xlnx→+∞,排除D选项;
令f(x)=0,得xlnx=0,所以x=1,即x>0时,函数图象与x轴只有一个交点,所以C选项满足题意.
故选:C.
又x>0时,f(x)=xlnx,容易判断,当x→+∞时,xlnx→+∞,排除D选项;
令f(x)=0,得xlnx=0,所以x=1,即x>0时,函数图象与x轴只有一个交点,所以C选项满足题意.
故选:C.
点评:函数图象问题就是考查函数性质的问题.不过,除了分析定义域、值域、单调性、奇偶性、极值与最值等性质外,还要注意对特殊点,零点等性质的分析,注意采用排除法等间接法解题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
以(-4,0),(4,0)为焦点,y=±
x为渐近线的双曲线的方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从1,2,3,4,5,6这六个数中,不放回地任意取两个数,每次取一个数,则所取的两个数都是偶数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
复数(1-i)2+(a-i)2是纯虚数,则实数a等于( )
| A、-1 | B、1 | C、±1 | D、0 |
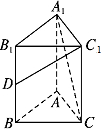 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为