题目内容
18.10、(文)若关于x的不等式x3-3x+3+a≤0恒成立,其中-2≤x≤3,则实数a的最大值为( )| A. | 1 | B. | -1 | C. | -5 | D. | -21 |
分析 问题转化为a≤-x3+3x-3在x∈[-2,3]恒成立,令f(x)=-x3+3x-3,x∈[-2,3],根据函数的单调性求出a的最大值即可.
解答 解:若关于x的不等式x3-3x+3+a≤0恒成立,
则a≤-x3+3x-3在x∈[-2,3]恒成立,
令f(x)=-x3+3x-3,x∈[-2,3],
则f′(x)=-3x2+3=-3(x+1)(x-1),
令f′(x)>0,解得:-1<x<1,
令f′(x)<0,解得:x>1或x<-1,
故f(x)在[-2,-1)递减,在(-1,1)递增,在(1,2]递减,
而 f(-2)=-1,f(-1)=-5,f(1)=-1,f(2)=-5,
故a≤-5,
故a的最大值是-5,
故选:C.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
相关题目
9.若函数f(x)=ax2-bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
7.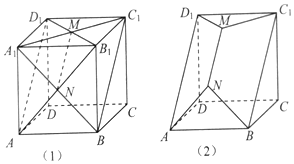 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{17}{24}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |