题目内容
17.一个棱长为$6\sqrt{2}$的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
分析 在一个棱长为6$\sqrt{2}$的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,说明正方体在正四面体的内切球内,求出内切球的直径,就是正方体的对角线的长,然后求出正方体的棱长.
解答 解:设球的半径为r,由正四面体的体积得:
4×$\frac{1}{3}×r×(6\sqrt{2})^{2}$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×(6\sqrt{2})^{2}×\sqrt{(6\sqrt{2})^{2}-(\frac{\sqrt{3}}{3}×6\sqrt{2})^{2}}$,
解得r=$\sqrt{3}$,
设正方体的最大棱长为a,
∴3a2=(2$\sqrt{3}$)2,解得a=2.
故选:C.
点评 本题是中档题,考查正四面体的内接球的知识,球的内接正方体的棱长的求法,考查空间想象能力,转化思想,计算能力.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
7.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y对x的线性回归方程为( )
| 父亲身高x/cm | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y/cm | 175 | 176 | 177 | 178 | 179 |
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=x+1 | C. | $\widehat{y}$=88+$\frac{1}{2}$x | D. | $\widehat{y}$=176 |
5.据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8~10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):

(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 天津 | 24 | 22 | 26 | 23 | 24 | 26 | 27 | 25 | 28 | 24 | 25 | 26 |
| 上海 | 32 | 27 | 33 | 31 | 30 | 31 | 32 | 33 | 30 | 32 | 30 | 30 |

(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).
12.点P(0,1)到双曲线$\frac{y^2}{4}-{x^2}=1$渐近线的距离是( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 5 |
9.若函数f(x)=ax2-bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
7.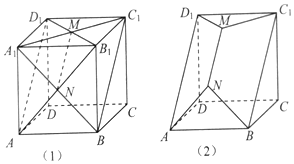 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{17}{24}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |