题目内容
已知函数f(sinx-cosx)=sinx•cosx,求f(
)的值.
| 1 |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:运用换元法,设出sinx-cosx,利用同角三角函数关系,整理求得函数解析式,进而把
代入即可.
| 1 |
| 2 |
解答:
解:令sinx-cosx=t,则sinx•cosx=
(sin2x+cos2x-t2)=
-
t2,
∴f(x)=
-
x2,
∴f(
)=
-
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
点评:本题主要考查了函数解析式的求法,同角三角函数关系式.解题的关键是求出函数的解析式.

练习册系列答案
相关题目
已知椭圆x2sinα-y2cosα=1(0≤α<2π)的焦点在y轴上,则α的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
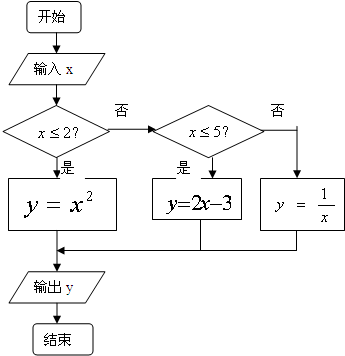 如图:
如图: