题目内容
设函数f(x)=
ax3+
bx2+(1-2a)x,a,b∈R,a≠0,
(Ⅰ)若曲线y=f(x)与x轴相切于异于原点的一点,且函数f(x)的极小值为-
a,求a,b的值;
(Ⅱ)若x0>0,且
+
+
=0,
①求证:af′(
)<0;
②求证:f(x)在(0,1)上存在极值点.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)若曲线y=f(x)与x轴相切于异于原点的一点,且函数f(x)的极小值为-
| 4 |
| 3 |
(Ⅱ)若x0>0,且
| a |
| x0+2 |
| b |
| x0+1 |
| 1-2a |
| x0 |
①求证:af′(
| x0 |
| x0+1 |
②求证:f(x)在(0,1)上存在极值点.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)依据题意得:f(x)=
x(x+
)2,令f′(x)=a(x+
)(x+
)=0,解出x,结合图形,得到极小值,解出方程即可得到a,b的值;
(Ⅱ)①f′(x)=ax2+bx+(1-2a),整理得到af′(
)=
<0;
②f′(0)=1-2a,f′(1)=1-a+b.对a分类讨论,依据①得到导数f′(
)的正负,再由函数零点的存在性定理,即可得证.
| a |
| 3 |
| 3b |
| 4a |
| 3b |
| 4a |
| b |
| 4a |
(Ⅱ)①f′(x)=ax2+bx+(1-2a),整理得到af′(
| x0 |
| x0+1 |
| -a2x0 |
| (x0+1)2(x0+2) |
②f′(0)=1-2a,f′(1)=1-a+b.对a分类讨论,依据①得到导数f′(
| x0 |
| x0+1 |
解答:
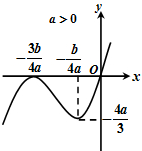 解:(Ⅰ)f(x)=
解:(Ⅰ)f(x)=
x[x2+
x+
],
依据题意得:f(x)=
x(x+
)2,且
=
≠0,
f′(x)=a(x+
)(x+
)=0,得x=-
或x=-
.
如图,得f(-
)=-
a,
∴
(-
)(-
+
)2=-
,则b=4a,
代入
=
得,b=
.
(Ⅱ)①证明:f′(x)=ax2+bx+(1-2a).
a f′(
)=a[a(
)2+
+(1-2a)]
=ax0[
+
+
]=ax0[
-
]=
<0.
②f′(0)=1-2a,f′(1)=1-a+b.
若0<a<
,则f′(0)=1-2a>0,由①知f′(
)<0,
所以f′(x)在(0,
)有零点,从而f(x)在(0,1)上存在极值点.
若a≥
,由①知f′(
)<0,
又f′(1)=1-a+b=1-a-
-
=
>0,
所以f′(x)在(0,
)有零点,从而f(x)在(0,1)上存在极值点.
若a<0,由①知f′(
)>0,f′(1)=1-a+b=
<0,
所以f′(x)在(0,
)有零点,从而f(x)在(0,1)上存在极值点.
综上知f(x)在(0,1)上存在极值点.
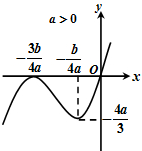 解:(Ⅰ)f(x)=
解:(Ⅰ)f(x)=| a |
| 3 |
| 3b |
| 2a |
| 3(1-2a) |
| a |
依据题意得:f(x)=
| a |
| 3 |
| 3b |
| 4a |
| 9b2 |
| 16a2 |
| 3-6a |
| a |
f′(x)=a(x+
| 3b |
| 4a |
| b |
| 4a |
| 3b |
| 4a |
| b |
| 4a |
如图,得f(-
| b |
| 4a |
| 4 |
| 3 |
∴
| a |
| 3 |
| b |
| 4a |
| b |
| 4a |
| 3b |
| 4a |
| 4a |
| 3 |
代入
| 9b2 |
| 16a2 |
| 3-6a |
| a |
| 4 |
| 5 |
(Ⅱ)①证明:f′(x)=ax2+bx+(1-2a).
a f′(
| x0 |
| x0+1 |
| x0 |
| x0+1 |
| bx0 |
| x0+1 |
=ax0[
| ax0 |
| (x0+1)2 |
| b |
| x0+1 |
| 1-2a |
| x0 |
| ax0 |
| (x0+1)2 |
| a |
| x0+2 |
| -a2x0 |
| (x0+1)2(x0+2) |
②f′(0)=1-2a,f′(1)=1-a+b.
若0<a<
| 1 |
| 2 |
| x0 |
| x0+1 |
所以f′(x)在(0,
| x0 |
| x0+1 |
若a≥
| 1 |
| 2 |
| x0 |
| x0+1 |
又f′(1)=1-a+b=1-a-
| a(x0+1) |
| x0+2 |
| (1-2a)(x0+1) |
| x0 |
| (3a-1)x0+2(2a-1) |
| (x0+2)x0 |
所以f′(x)在(0,
| x0 |
| x0+1 |
若a<0,由①知f′(
| x0 |
| x0+1 |
| (3a-1)x0+2(2a-1) |
| (x0+2)x0 |
所以f′(x)在(0,
| x0 |
| x0+1 |
综上知f(x)在(0,1)上存在极值点.
点评:本题以函数为载体,考查导数知识的运用,考查曲线的切线,同时考查零点存在性定理,综合性比较强.

练习册系列答案
相关题目
在如图所示的程序框图中,输入f0(x)=cosx,则输出的是( )
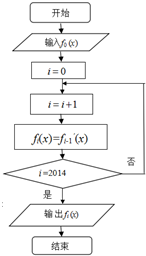

| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
阅读如图的程序框图,运行相应的程序,输出的结果为( )


| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、2 |
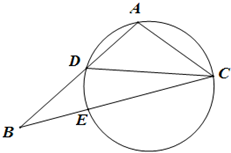 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=