题目内容
给定一组函数解析式:①y=x
;②y=x
;③y=x-
;④y=x-
;⑤y=x
;⑥y=x-
;⑦y=x
,如图所示一组函数图象.图象对应的解析式号码顺序正确的是( )
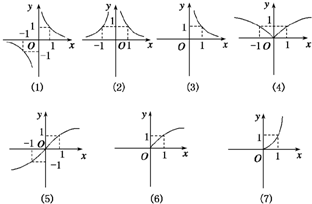
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |

| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:分别判断每一个幂函数的性质,即可得到对应的函数图象关系.
解答:
解:观察前三个图象,由于在第一象限内,函数值随x的增大而减小,知幂指数应小于零,其中第一个函数图象关于原点对称,
第二个函数图象关于y轴对称,而第三个函数的定义域为x>0,
因此,第一个图象应对应函数y=x-
,第三个图象对应y=x-
;
后四个图象都通过(0,0)和(1,1)两点,故知幂指数应大于0,
第四个图象关于y轴对称,第五个图象关于原点对称,定义域都是R,
因此,第四个图象对应函数y=x
;第五个图象对应y=x
,
由最后两个图象知函数定义域为x≥0,而第六个图象呈上凸状,幂指数应小于1,第七个图象呈下凹状,幂指数应大于1,故第六个图象对应y=x
,
第七个图象对应y=x
.
故选:C.
第二个函数图象关于y轴对称,而第三个函数的定义域为x>0,
因此,第一个图象应对应函数y=x-
| 1 |
| 3 |
| 3 |
| 2 |
后四个图象都通过(0,0)和(1,1)两点,故知幂指数应大于0,
第四个图象关于y轴对称,第五个图象关于原点对称,定义域都是R,
因此,第四个图象对应函数y=x
| 2 |
| 3 |
| 1 |
| 3 |
由最后两个图象知函数定义域为x≥0,而第六个图象呈上凸状,幂指数应小于1,第七个图象呈下凹状,幂指数应大于1,故第六个图象对应y=x
| 3 |
| 4 |
第七个图象对应y=x
| 3 |
| 2 |
故选:C.
点评:本题主要考查幂函数的图象和性质,比较基础.

练习册系列答案
相关题目
已知某几何体的三视图(单位:dm)如图所示,则该几何体的体积是( )


A、
| ||
B、
| ||
| C、1dm3 | ||
D、
|
执行如图所示的程序框图,输入m=828,n=345,则输出的实数m的值是( )


| A、68 | B、69 |
| C、138 | D、139 |
阅读如图的程序框图,运行相应的程序,输出的结果为( )


| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、2 |
一个几何体的三视图如图所示(单位:cm),则该几何体的体积为( )


A、(32+
| ||
B、(32+
| ||
C、(41+
| ||
D、(41+
|