题目内容
4.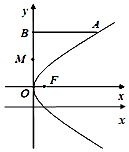 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M(Ⅰ)求抛物线的标准方程;
(Ⅱ)以点M为圆心,MB为半径作圆M.当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
分析 (Ⅰ)求出双曲线4x2-12y2=3的右焦点坐标,即可求抛物线的标准方程;
(Ⅱ)求出圆心M(0,2)到直线AK的距离,即可讨论直线AK与圆M的位置关系.
解答 解:(Ⅰ)设双曲线4x2-12y2=3的右焦点坐标为F(c,0),
由4x2-12y2=3得$\frac{x^2}{{\frac{3}{4}}}-\frac{y^2}{{\frac{1}{4}}}=1$,∴$c=\sqrt{\frac{3}{4}+\frac{1}{4}}=1$.(2分)
∴$\frac{p}{2}=1$,即p=2,故抛物线的标准方程为y2=4x.(4分)
(Ⅱ)∵点A的横坐标为4,且位于x轴上方的点,∴y=4
∴点A的坐标是(4,4),由题意得B(0,4),M(0,2).(5分)
∴圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时直线AK与圆M相离.(6分)
当m≠4时,直线AK的方程为$y=\frac{4}{4-m}(x-m)$,
即为4x-(4-m)y-4m=0.(7分)
圆心M(0,2)到直线AK的距离为$d=\frac{{|{2m+8}|}}{{\sqrt{16+{{(m-4)}^2}}}}$,(8分)
令d>2,解得m>1.(9分)
∴当m>1时,直线AK与圆M相离;((10分))
当m=1时,直线AK与圆M相切; (11分)
当m<1时,直线AK与圆M相交.(12分)
点评 本题考查双曲线、抛物线的方程与性质,考查直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
14.已知焦点在x轴上的双曲线渐近线方程为$y=±\frac{2}{3}x$,则此双曲线的离心率等于( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
15.设$\frac{i}{1+i}=x+yi$(x,y∈R,i为虚数单位),则模|x-yi|=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
19.设命题p:直线x-y+1=0的倾斜角为135°;命题q:平面直角坐标系内的三点A(-1,-3),B(1,1),C(2,2)共线.则下列判断正确的是( )
| A. | ¬p为假 | B. | ¬p∧¬q为真 | C. | p∨q为真 | D. | q为真 |
16.为了了解800名高三学生是否喜欢背诵诗词,从中抽取一个容量为20的样本,若采用系统抽样,则分段的间隔k为( )
| A. | 50 | B. | 60 | C. | 30 | D. | 40 |
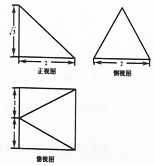 某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2)
某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2)