题目内容
15.设$\frac{i}{1+i}=x+yi$(x,y∈R,i为虚数单位),则模|x-yi|=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 利用复数代数形式的乘除运算化简等式左边,再由复数相等的条件求得x,y值,最后代入复数模的公式求得答案.
解答 解:∵$\frac{i}{1+i}=\frac{i(1-i)}{(1+i)(1-i)}=\frac{1}{2}+\frac{i}{2}=x+yi$,
∴x=y=$\frac{1}{2}$,
则|x-yi|=|$\frac{1}{2}-\frac{i}{2}$|=$\sqrt{(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}=\frac{\sqrt{2}}{2}$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.△ABC的三边长分别是a,b,c,且a=1,B=45°,S△ABC=2,则△ABC的外接圆的面积为( )
| A. | 25π | B. | 5π | C. | $\frac{25π}{2}$ | D. | $\frac{5π}{2}$ |

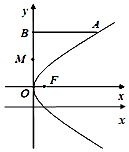 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M