题目内容
14.函数f(x)=sinxcosx的值域是[-$\frac{1}{2}$,$\frac{1}{2}$].分析 利用正弦的二倍角公式对函数解析式化简,进而根据sin2x的范围求得函数的值域.
解答 解:∵f(x)=sinxcosx=$\frac{1}{2}$sin2x,
又∵-1≤sin2x≤1
∴f(x)=$\frac{1}{2}$sin2x∈[-$\frac{1}{2}$,$\frac{1}{2}$].
故答案为:[-$\frac{1}{2}$,$\frac{1}{2}$].
点评 本题主要考查了二倍角的正弦.属基础题.

练习册系列答案
相关题目
2.已知变量x,y有如表中的观察数据,得到y对x的回归方程是$\widehaty=0.83x+a$,则其中a的值是( )
| x | 0 | 1 | 3 | 4 |
| y | 2.4 | 4.5 | 4.6 | 6.5 |
| A. | 2.64 | B. | 2.84 | C. | 3.95 | D. | 4.35 |
9.定义:分子为1且分母为正整数的分数为单位分数,我们可以把1拆为若干个不同的单位分数之和.如:1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$,1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$,1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$,以此类推,可得:1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$,其中a<b,a,b∈N*,设1≤x≤a,1≤y≤b,则$\frac{x+y+4}{x+2}$的最小值为( )
| A. | $\frac{25}{3}$ | B. | $\frac{23}{7}$ | C. | $\frac{8}{7}$ | D. | $\frac{6}{5}$ |
19.函数y=x2在P(1,1)处的切线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行,则双曲线的离心率是( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
6.某校高三共有男生400名,从所有高三男生中随机抽取20名男生测量身高(单位:cm)作为样本,得到频率分布表与频率分布直方图1(部分)如表:
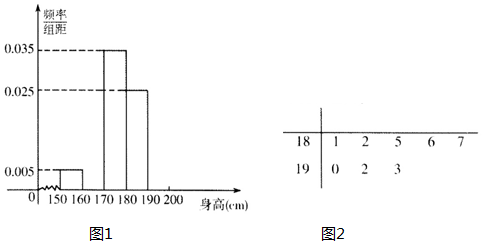
(Ⅰ)求n1、n2、f1、f2;
(Ⅱ)试估计身高不低于180cm的该校高三男生人数,并说明理由;
(Ⅲ)从样本中不低于180cm的男生身高,绘制成茎叶图(图2);
现从身高不低于185cm的男生中任取3名参加选拔性测试,求至少有两位身高不低于190cm的概率.
| 分组 | 频数 | 频率 |
| [150,160) | 1 | |
| [160,170) | n1 | f1 |
| [170,180) | n2 | f2 |
| [180,190) | 5 | |
| [190,200] | 3 |

(Ⅰ)求n1、n2、f1、f2;
(Ⅱ)试估计身高不低于180cm的该校高三男生人数,并说明理由;
(Ⅲ)从样本中不低于180cm的男生身高,绘制成茎叶图(图2);
现从身高不低于185cm的男生中任取3名参加选拔性测试,求至少有两位身高不低于190cm的概率.
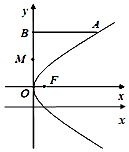 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M