题目内容
14.已知焦点在x轴上的双曲线渐近线方程为$y=±\frac{2}{3}x$,则此双曲线的离心率等于( )| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
分析 求出双曲线的渐近线方程,可得2a=3b,再由a,b,c的关系以及离心率公式计算即可得到.
解答 解:焦点在x轴上的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
由题意可得,$\frac{b}{a}$=$\frac{2}{3}$,
即b=$\frac{2}{3}$a,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+\frac{4}{9}{a}^{2}}$=$\frac{\sqrt{13}}{3}$a,
即有e=$\frac{c}{a}$=$\frac{\sqrt{13}}{3}$.
故选:D.
点评 本题考查双曲线的方程和性质,考查渐近线方程和离心率的求法,属于基础题.

练习册系列答案
相关题目
4.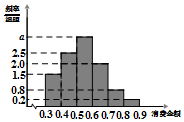 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )| A. | 2000 | B. | 4500 | C. | 6000 | D. | 7500 |
9.已知等差数列{an}的前7项和为14,则${e^{a_2}}•{e^{a_3}}•{e^{a_5}}•{e^{a_6}}$=( )
| A. | e2 | B. | e4 | C. | e8 | D. | e16 |

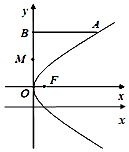 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M