题目内容
19.设命题p:直线x-y+1=0的倾斜角为135°;命题q:平面直角坐标系内的三点A(-1,-3),B(1,1),C(2,2)共线.则下列判断正确的是( )| A. | ¬p为假 | B. | ¬p∧¬q为真 | C. | p∨q为真 | D. | q为真 |
分析 先判断命题p,命题q的真假,进而根据复合命题真假判断的真值表,得到结论.
解答 解:直线x-y+1=0的斜率为1,倾斜角为45°,
故命题p为假命题;
直线AB的斜率为2,直线BC的斜率为1,故三点A(-1,-3),B(1,1),C(2,2)不共线.
故命题q为假命题,
故¬p为真命题,故A错误;
¬p∧¬q为真命题,故B正确;
p∨q为假命题,故C错误;
q为为假命题,故D错误;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了复合命题,直线的倾斜角,三点共线等知识点,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知等差数列{an}的前7项和为14,则${e^{a_2}}•{e^{a_3}}•{e^{a_5}}•{e^{a_6}}$=( )
| A. | e2 | B. | e4 | C. | e8 | D. | e16 |
10.△ABC的三边长分别是a,b,c,且a=1,B=45°,S△ABC=2,则△ABC的外接圆的面积为( )
| A. | 25π | B. | 5π | C. | $\frac{25π}{2}$ | D. | $\frac{5π}{2}$ |
9.定义:分子为1且分母为正整数的分数为单位分数,我们可以把1拆为若干个不同的单位分数之和.如:1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$,1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$,1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$,以此类推,可得:1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$,其中a<b,a,b∈N*,设1≤x≤a,1≤y≤b,则$\frac{x+y+4}{x+2}$的最小值为( )
| A. | $\frac{25}{3}$ | B. | $\frac{23}{7}$ | C. | $\frac{8}{7}$ | D. | $\frac{6}{5}$ |
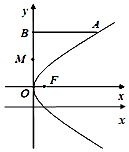 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M