��Ŀ����
����������k��3��������Ϊk������{an}���㣺�������i=1��2������k������ai��
������Sk=a1+a2+��+ak�����������{an}Ϊ�������С���
���������-1��3��5��2��4��
��
��
�Ƿ��ǡ������С�����˵�����ɣ�
������{an}Ϊ�������С�����֤��ai��0��i=1��2������k�������
������{bn}�ǹ���Ϊd��������Ȳ����У����������������m��3��b1��b2������bm�����ɡ������С�����{bn}�Ĺ���d��
| Sk |
| k-1 |
���������-1��3��5��2��4��
| 3 |
| 4 |
| 32 |
| 42 |
| 33 |
| 43 |
������{an}Ϊ�������С�����֤��ai��0��i=1��2������k�������
������{bn}�ǹ���Ϊd��������Ȳ����У����������������m��3��b1��b2������bm�����ɡ������С�����{bn}�Ĺ���d��
���㣺���е����
ר�⣺�Ȳ�������ȱ�����
�����������ݡ������С��Ķ��壬�����ж�����-1��3��5��2��4��
��
��
�Ƿ��ǡ������С���
������{an}Ϊ�������С������÷�֤������֤����ai��0��i=1��2������k�������
����
| 3 |
| 4 |
| 32 |
| 42 |
| 33 |
| 43 |
������{an}Ϊ�������С������÷�֤������֤����ai��0��i=1��2������k�������
����
���
�⣺������Ϊ
=
��5������-1��3��5��2��4���ǡ������У�
����Ϊ
=
��
����
������
��
��
������
��������
��
��
�ǡ������С���
����֤��֤����
�������ij��ai��0����
a1+a2+��+ai-1+ai+1+��+ak-1+ak=Sk-ai��Sk��
��aj=max{a1��a2����ai-1��ai+i����ak-1+ak}��
��Sk-ai=a1+a2+��+ai-1+ai+1+��+ak-1+ak�ܣ�k-1��aj��
���ԣ�k-1��aj��Sk����aj��
��
���롰�����С�����ì�ܣ�����ԭ������ȷ��
�����ɣ����ʿ�֪b1��0��d��0��
�ٵ�d=0ʱ��b1=b2=��=bm=
��
���������裻
�ڵ�d��0ʱ��b1��b2������bm��
�ɡ������С��Ķ����֪bm��
������m-1��[b1+��m-1��d]��mb1+
m��m-1��d��
�����ã�m-1����m-2��d��2b1��*��
��Ȼ��m=2b1+3ʱ����������ʽ��*���Ͳ�����
����d��0ʱ��������������m��3����m-1����m-2��d��2b1�����ܶ�������
�������ۿ�֪{bn}�Ĺ���d=0��
| S5 |
| 5-1 |
| 13 |
| 4 |
����Ϊ
| S3 |
| 3-1 |
| 111 |
| 128 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 32 |
| 42 |
| 33 |
| 43 |
��������
| 3 |
| 4 |
| 32 |
| 42 |
| 33 |
| 43 |
����֤��֤����
�������ij��ai��0����
a1+a2+��+ai-1+ai+1+��+ak-1+ak=Sk-ai��Sk��
��aj=max{a1��a2����ai-1��ai+i����ak-1+ak}��
��Sk-ai=a1+a2+��+ai-1+ai+1+��+ak-1+ak�ܣ�k-1��aj��
���ԣ�k-1��aj��Sk����aj��
| Sk |
| k-1 |
���롰�����С�����ì�ܣ�����ԭ������ȷ��
�����ɣ����ʿ�֪b1��0��d��0��
�ٵ�d=0ʱ��b1=b2=��=bm=
| Sm |
| m |
| Sm |
| m-1 |
�ڵ�d��0ʱ��b1��b2������bm��
�ɡ������С��Ķ����֪bm��
| Sm |
| m-1 |
| 1 |
| 2 |
�����ã�m-1����m-2��d��2b1��*��
��Ȼ��m=2b1+3ʱ����������ʽ��*���Ͳ�����
����d��0ʱ��������������m��3����m-1����m-2��d��2b1�����ܶ�������
�������ۿ�֪{bn}�Ĺ���d=0��
������������Ҫ���������¶����Ӧ�ã���ȷ���⡰�����С��Ķ����ǽ������Ĺؼ����ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
�����Ŀ
 ��ͼ����֪������ABCD-A1B1C1D1���ⳤΪ2��MΪ������AA1D1D�����ģ�NΪ��AB���е㣮
��ͼ����֪������ABCD-A1B1C1D1���ⳤΪ2��MΪ������AA1D1D�����ģ�NΪ��AB���е㣮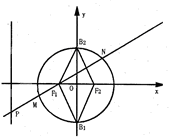 ��ͼ����ԲC��
��ͼ����ԲC��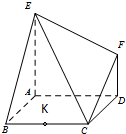 ��ͼ����֪������EABCDF�ĵ���ABCD�DZ߳�Ϊ2�������Σ�EA�͵���ABCD��FD��EA����FD=
��ͼ����֪������EABCDF�ĵ���ABCD�DZ߳�Ϊ2�������Σ�EA�͵���ABCD��FD��EA����FD=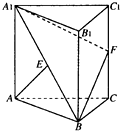 ��ͼ��������ABC-A1B1C1�IJ���AA1��ƽ��ABC����ABCΪ�ȱ������Σ�����AA1C1C�������Σ�E��A1B���е㣬F����CC1�ϵĵ㣮
��ͼ��������ABC-A1B1C1�IJ���AA1��ƽ��ABC����ABCΪ�ȱ������Σ�����AA1C1C�������Σ�E��A1B���е㣬F����CC1�ϵĵ㣮