题目内容
已知cos(π-α)=-
,
<α<2π,则sin(2π-α)= .
| 1 |
| 2 |
| 3π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式与同角三角函数间的关系即可求得答案.
解答:
解:∵cos(π-α)=-cosα=-
,
∴cosα=
,又
<α<2π,
∴sin(2π-α)=-sinα=-(-
)=
,
故答案为:
.
| 1 |
| 2 |
∴cosα=
| 1 |
| 2 |
| 3π |
| 2 |
∴sin(2π-α)=-sinα=-(-
| 1-cos2α |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查诱导公式与同角三角函数间的关系的应用,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
在极坐标系中,圆ρ=2sinθ的圆心到极轴的距离为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
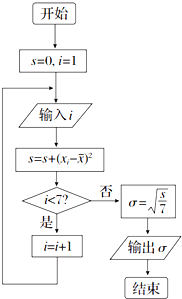 在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表:
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表: