题目内容
4.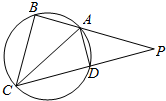 如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC
如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC(Ⅰ)求证:PD=2AB;
(Ⅱ)当BC=2,PC=5时.求AB的长.
分析 (Ⅰ)证明:△APD∽△CPB,利用AB=AD,BP=2BC,证明PD=2AB;
(Ⅱ)利用割线定理求AB的长.
解答 (Ⅰ)证明:∵四边形ABCD是圆内接四边形,
∴∠PAD=∠PCB,
∴∠APD=∠CPB,
∴△APD∽△CPB,
∴$\frac{PD}{PB}$=$\frac{AD}{CB}$,
∵BP=2BC
∴PD=2AD,
∴AB=AD,
∴PD=2AB;
(Ⅱ)解:由题意,BP=2BC=4,设AB=t,由割线定理得PD•PC=PA•PB,
∴2t×5=(4-t)×4
∴t=$\frac{8}{7}$,即AB=$\frac{8}{7}$.
点评 本题考查三角形相似的判断,考查割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
15.已知等差数列{an}满足a3+a9=2,则a6=( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
12.动点P到点M(3,0)及点N(1,0)的距离之差为2,则点P的轨迹是( )
| A. | 双曲线 | B. | 双曲线的一支 | C. | 两条射线 | D. | 一条射线 |
19.已知tanx=$\frac{1}{2}$,则sin2($\frac{π}{4}$+x)=( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
9.在△ABC中,若a2-b2=c(b+c),则A=( )
| A. | 60° | B. | 120° | C. | 45° | D. | 30° |
16.如图点P在平面区域$\left\{\begin{array}{l}{2x-y+2≥0}\\{x-2y+1≤0}\\{x+y-2≤0}\end{array}\right.$上,点Q在曲线x2+(y+$\frac{3}{2}$)2=1上,那么|PQ|的最小值为( )
| A. | $\sqrt{5}$-1 | B. | $\frac{4}{\sqrt{5}}$-1 | C. | 2$\sqrt{2}$-1 | D. | $\frac{\sqrt{13}}{2}$-1 |