题目内容
16.如图点P在平面区域$\left\{\begin{array}{l}{2x-y+2≥0}\\{x-2y+1≤0}\\{x+y-2≤0}\end{array}\right.$上,点Q在曲线x2+(y+$\frac{3}{2}$)2=1上,那么|PQ|的最小值为( )| A. | $\sqrt{5}$-1 | B. | $\frac{4}{\sqrt{5}}$-1 | C. | 2$\sqrt{2}$-1 | D. | $\frac{\sqrt{13}}{2}$-1 |
分析 由约束条件作出可行域,画出圆,再由点到直线的距离公式求出圆心到直线x-2y+1=0的距离,则|PQ|的最小值可求.
解答  解:由题意画出图形如图:
解:由题意画出图形如图:
圆x2+(y+$\frac{3}{2}$)2=1的圆心(0,-$\frac{3}{2}$)到直线x-2y+1=0的距离为d=$\frac{|-2×(-\frac{3}{2})+1|}{\sqrt{5}}=\frac{4}{\sqrt{5}}$,
∴|PQ|的最小值为$\frac{4}{\sqrt{5}}-1$.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知全集为自然数集合N,集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩(∁UB)=( )
| A. | {3,5,7} | B. | {1,5,7} | C. | {1,3,9} | D. | {1,2,3} |
7.“a>b,c>0”是“ac>bc”的( )条件.
| A. | 必要不充分 | B. | 充分不必要 | ||
| C. | 充要 | D. | 既不充分也不必要 |
11.已知x>0,y>0,且$\frac{1}{x}+\frac{2}{y}$=1,若2x+y>t2+2t恒成立,则实数t的取值范围是( )
| A. | [-4,2] | B. | (-4,2) | C. | (0,2) | D. | (0,4) |
1.已知U=R,函数y=ln(1-x)的定义域为M,集合N={x|0<x<2},则M∩(∁UN)=( )
| A. | (-∞,0] | B. | (0,1) | C. | [1,2) | D. | [2,+∞) |
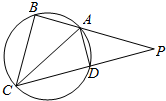 如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC
如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC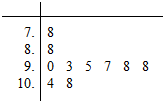 某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.
某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.