��Ŀ����
14������˵����ȷ�ĸ����ǣ�����������f��x��=$\frac{1}{{2}^{x}+1}$+aΪ�溯������a=$\frac{1}{2}$��
�ڡ��ڡ�ABC�У���sinA��sinB����A��B�����������Ǽ����⣻
�ۡ�������a��b��c�ɵȱ����С��ǡ�b=$\sqrt{ac}$���ļȲ����Ҳ����Ҫ������
�����⡰?x��R��x3-x2+1��0���ķ��ǡ�?x0��R��x03-x02+1��0����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ���ú�������ż���жϢٵ��������������������Ҷ����жϢڵ��������ó�Ҫ�����жϢ۵���������ķ��жϢܵ�����
��� �⣺���ڢ٣���f��x��=$\frac{1}{{2}^{x}+1}$+aΪ�溯������f��0��=0�����a=-$\frac{1}{2}$�����Ԣٲ���ȷ��
���ڢڣ����ڡ�ABC�У���sinA��sinB�������Ҷ����ɵ�a��b����A��B�������������������⣻���Ԣڲ���ȷ��
���ڢۣ���������a��b��c�ɵȱ����С���b2=ac����b=��$\sqrt{ac}$��
��a=b=c=0������b=$\sqrt{ac}$����������a��b��c�ɵȱ����в�������
�ࡰ������a��b��c�ɵȱ����С��ǡ�b=$\sqrt{ac}$���ļȲ����Ҳ����Ҫ���������Ԣ���ȷ��
���ڢܣ����⡰?x��R��x3-x2+1��0���ķ��ǡ�?x0��R��x03-x02+1��0������������ķ���ʽ�����Ԣ���ȷ��
��ѡ��C��
���� ���⿼������ķ���Ҫ�������������ٵ��ж���Ӧ�ã�����֪ʶ�Ŀ��飮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
5����֪ԲO��x2+y2=1��ֱ��l���㣨-2��0������ֱ��l������һ�㵽Բ�ľ������Сֵ����Բ�İ뾶����ֱ��l��б��Ϊ��������
| A�� | $��\frac{{\sqrt{3}}}{3}$ | B�� | ��3 | C�� | $��\sqrt{2}$ | D�� | ��1 |
19������z=$\frac{2+i}{i}$=��������
| A�� | 1-2i | B�� | 1+2i | C�� | -1-2i | D�� | -1+2i |
6����֪ȫ��Ϊ��Ȼ������N������A={1��3��5��7��9}��B={0��3��6��9��12}����A�ɣ�∁UB��=��������
| A�� | {3��5��7} | B�� | {1��5��7} | C�� | {1��3��9} | D�� | {1��2��3} |
 ��ͼ���ڱ߳�Ϊ3����������������A����Ӱ������ʾ��������ͬѧ�����ģ��ķ���������A���������ÿ������������ÿ���������10000���㣬����¼��������A�ڵĵ�ĸ���������������飬�������������A�ڵ�ĸ���ƽ��ֵΪ6600����������A�����ԼΪ��������
��ͼ���ڱ߳�Ϊ3����������������A����Ӱ������ʾ��������ͬѧ�����ģ��ķ���������A���������ÿ������������ÿ���������10000���㣬����¼��������A�ڵĵ�ĸ���������������飬�������������A�ڵ�ĸ���ƽ��ֵΪ6600����������A�����ԼΪ��������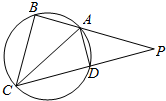 ��ͼ���ı���ABCD��Բ�ڽ��ı��Σ�BA��CD���ӳ��߽��ڵ�P����AB=AD��BP=2BC
��ͼ���ı���ABCD��Բ�ڽ��ı��Σ�BA��CD���ӳ��߽��ڵ�P����AB=AD��BP=2BC