题目内容
14.已知奇函数f(x)满足f(x+2)=f(x),当x∈[0,1]时.,f(x)=x,则当x∈[k,k+1](k∈Z)时,函数f(x)的解析式是f(x)=$\left\{\begin{array}{l}{x-k,k是偶数}\\{x-k-1,k是奇数}\end{array}\right.$.分析 由题意,函数的周期为2.x∈[-1,0]时,f(x)=x,分k的奇数、偶数讨论,即可得出结论.
解答 解:由题意,函数的周期为2.x∈[-1,0]时,f(x)=x
k=2n时,x∈[k,k+1],x-k∈[0,1],f(x)=f(x-k)=x-k;
k=2n-1,x-k-1∈[-1,0],f(x)=f(x-k-1)=x-k-1;
∴f(x)=$\left\{\begin{array}{l}{x-k,k是偶数}\\{x-k-1,k是奇数}\end{array}\right.$.
故答案为:f(x)=$\left\{\begin{array}{l}{x-k,k是偶数}\\{x-k-1,k是奇数}\end{array}\right.$.
点评 本题主要考查函数奇偶性与单调性的综合应用,函数的周期性,利用函数奇偶性和周期性是解决本题的关键.

练习册系列答案
相关题目
19.已知二次函数f(x)满足f(1+x)=f(2015-x),且f(x)=0有两个实数根x1,x2,则x1+x2等于( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 不确定 |
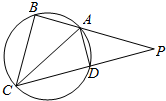 如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC
如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC