题目内容
已知△ABC和点M满足2
+
+
=0．若存在实m使得
+
=m
成立，则m=（ ）
| MA |
| MB |
| MC |
| AB |
| AC |
| AM |
| A、2 | B、3 | C、4 | D、5 |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
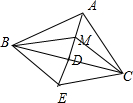
分析：如图所示，以MB，MB为邻边作平行四边形MBEC，可得
+
=
．由2
+
+
=
，可得
+
=-2
．可得
=-2
=2
．又
+
=2
，
+
=m
，即可得出．
| MB |
| MC |
| ME |
| MA |
| MB |
| MC |
| 0 |
| MB |
| MC |
| MA |
| ME |
| MA |
| MD |
| AB |
| AC |
| AD |
| AB |
| AC |
| AM |
解答：
解：如图所示，以MB，MB为邻边作平行四边形MBEC，
可得
+
=
．
由2
+
+
=
．
可得
+
=-2
．
∴
=-2
=2
．
∴点M为线段AD的中点，
又
+
=2
，
+
=m
，
∴m=4．
故选：C．
可得
| MB |
| MC |
| ME |
由2
| MA |
| MB |
| MC |
| 0 |
可得
| MB |
| MC |
| MA |
∴
| ME |
| MA |
| MD |
∴点M为线段AD的中点，
又
| AB |
| AC |
| AD |
| AB |
| AC |
| AM |
∴m=4．
故选：C．
点评：本题考查了向量平行四边形法则、向量共线定理、向量基本定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
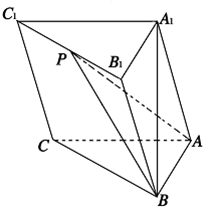如图，在三棱柱ABC-A1B1C1中，AB⊥AC，AC⊥BB1，AB=A1B=AC=1，BB1=