题目内容
已知D、E分别是△ABC边AB、AC上的点，且BD=2AD，AE=2EC，点P是线段DE上的任意一点，若
=x
+y
，则xy的最大值为 ．
| AP |
| AB |
| AC |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：BD=2AD，AE=2EC，点P是线段DE上的任意一点，
=x
+y
，可得
=3x
+
，利用向量共线定理可得3x+
=1，再利用基本不等式的性质即可得出．
| AP |
| AB |
| AC |
| AP |
| AD |
| 3y |
| 2 |
| AE |
| 3y |
| 2 |
解答：
解：如图所示，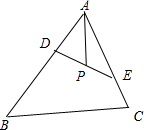
∵BD=2AD，AE=2EC，点P是线段DE上的任意一点，
=x
+y
，
∴
=3x
+
，
∴3x+
=1，
∴2x+y=
．
∵x，y＞0，
∵
≥2
，
xy≤
，当且仅当y=2x=
时取等号．
则xy的最大值为
．
故答案为：
．
∵BD=2AD，AE=2EC，点P是线段DE上的任意一点，
| AP |
| AB |
| AC |
∴
| AP |
| AD |
| 3y |
| 2 |
| AE |
∴3x+
| 3y |
| 2 |
∴2x+y=
| 2 |
| 3 |
∵x，y＞0，
∵
| 2 |
| 3 |
| 2xy |
xy≤
| 1 |
| 18 |
| 1 |
| 3 |
则xy的最大值为
| 1 |
| 18 |
故答案为：
| 1 |
| 18 |
点评：本题考查了向量共线定理、基本不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知△ABC和点M满足2
+
+
=0．若存在实m使得
+
=m
成立，则m=（ ）
| MA |
| MB |
| MC |
| AB |
| AC |
| AM |
| A、2 | B、3 | C、4 | D、5 |
已知A、B、C三点不共线，对平面ABC外的任一点O，下列条件中能确定定点M与点A、B、C一定共面的是（ ）
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
已知椭圆C：