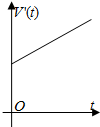题目内容
已知函数f(x)=(a-x)ex+b,曲线y=f(x)在点(1,f(1))处的切线方程为ex+y+1-e=0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=
,求证:存在x0≠0,使得g(x0)>1-
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=
| f(x) |
| x |
| 2 |
| e |
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:导数的概念及应用,导数的综合应用
分析:(Ⅰ)求出函数的导数,由题意可得f(1)=-1,且f′(1)=-e,列方程,解得a,b,即可得到f(x)的解析式;
(Ⅱ)求出g(x)的导数,设g′(x)=0的一个根为x0,运用零点存在定理,可得-2<x0<-1,即x0为g(x)的极大值点,而g(-1)=1-
,即可得证.
(Ⅱ)求出g(x)的导数,设g′(x)=0的一个根为x0,运用零点存在定理,可得-2<x0<-1,即x0为g(x)的极大值点,而g(-1)=1-
| 2 |
| e |
解答:
(Ⅰ)解:函数f(x)=(a-x)ex+b的导数为f′(x)=(a-x-1)ex,
曲线y=f(x)在点(1,f(1))处的切线方程为ex+y+1-e=0,
即有f(1)=-1,且f′(1)=-e,
即(a-1)e+b=-1且(a-2)e=-e,
解得a=1,b=-1,
即有f(x)=(1-x)ex-1;
(Ⅱ)证明:g(x)=
=
,
g′(x)=
,
设g′(x)=0的一个根为x0,
由于g′(-2)=
>0,g′(-1)=1-3e-1<0,
即有-2<x0<-1,
即x0为g(x)的极大值点,
而g(-1)=1-
.
故存在x0≠0,使得g(x0)>1-
.
曲线y=f(x)在点(1,f(1))处的切线方程为ex+y+1-e=0,
即有f(1)=-1,且f′(1)=-e,
即(a-1)e+b=-1且(a-2)e=-e,
解得a=1,b=-1,
即有f(x)=(1-x)ex-1;
(Ⅱ)证明:g(x)=
| f(x) |
| x |
| (1-x)ex-1 |
| x |
g′(x)=
| 1-ex(x2-x+1) |
| x2 |
设g′(x)=0的一个根为x0,
由于g′(-2)=
| 1-e-2(4+2+1) |
| 4 |
即有-2<x0<-1,
即x0为g(x)的极大值点,
而g(-1)=1-
| 2 |
| e |
故存在x0≠0,使得g(x0)>1-
| 2 |
| e |
点评:本题考查导数的运用:求切线方程和单调区间及极值,运用函数的零点存在定理是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
把五个标号为1到5的小球全部放入标号为1到4的四个盒子中,不许有空盒且任意一个小球都不能放入标有相同标号的盒子中,则不同的放法有( )
| A、36种 | B、45种 |
| C、54种 | D、84种 |
已知△ABC和点M满足2
+
+
=0.若存在实m使得
+
=m
成立,则m=( )
| MA |
| MB |
| MC |
| AB |
| AC |
| AM |
| A、2 | B、3 | C、4 | D、5 |
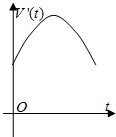
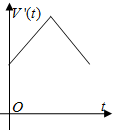
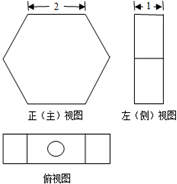 一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )
一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )