题目内容
双曲线
-
=1的焦点坐标为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、(-
| ||||
B、(0,-
| ||||
| C、(-5,0)、(5,0) | ||||
| D、(0,-5)、(0,5) |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线的方程和性质即可得到结论.
解答:
解:由双曲线的方程可知,a2=16,b2=9,
则c2=a2+b2=25,即c=5,
故双曲线的焦点坐标为:(±5,0),
故选:C.
则c2=a2+b2=25,即c=5,
故双曲线的焦点坐标为:(±5,0),
故选:C.
点评:本题主要考查双曲线的性质和方程,根据a,b,c之间的关系是解决本题的关键.

练习册系列答案
相关题目
不等式(x-3)(x-1)<0的解集是( )
| A、{x|1<x<3} |
| B、{x|x<1或x>3} |
| C、{x|x<1} |
| D、{x|x>3} |
为了得到函数y=sin(
x-
)的图象,只需将y=sin
x图象上的每个点纵坐标不变,横坐标( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
则回归直线方程可能是( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知动点P(t,t),Q(10-t,0),其中0<t<10,则点M(6,1),N(4,5)与直线PQ的关系是( )
| A、M,N均在直线PQ上 |
| B、M,N均不在直线PQ上 |
| C、M不在直线PQ上,N可能在直线PQ上 |
| D、M可能在直线PQ上,N不在直线PQ上 |
下列选项中两个函数相同的是( )
A、y=x,y=
| ||||||
B、y=|x|,y=
| ||||||
| C、y=1,y=x0 | ||||||
D、y=
|
已知实数x,y满足
,则目标函数z=x+2y的最大值为( )
|
| A、1 | ||
B、
| ||
| C、4 | ||
| D、5 |
椭圆
+
=1的离心率为( )
| x2 |
| 100 |
| y2 |
| 36 |
A、
| ||
B、
| ||
C、
| ||
D、
|
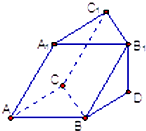 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )