题目内容
已知集合M={x|(x-1)2<4,x∈R},N={-2.-1,0,1,2},则M∩N=( )
| A、{0,1,2} |
| B、{-1,0,1,2} |
| C、{-1,0,2,3} |
| D、{0,1,2,3} |
考点:交集及其运算
专题:集合
分析:求出M中不等式的解集确定出M,找出M与N的交集即可.
解答:
解:由M中不等式变形得:-2<x-1<2,
解得:-1<x<3,即M=(-1,3),
∵N={-2.-1,0,1,2},
∴M∩N={0,1,2}.
故选:A.
解得:-1<x<3,即M=(-1,3),
∵N={-2.-1,0,1,2},
∴M∩N={0,1,2}.
故选:A.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在△ABC中,
=
,
=
,
=
,且满足:|
|=1,|
|=2,|
|=
,则
•
+
•
+
•
的值为( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| c |
| 3 |
| a |
| b |
| b |
| c |
| c |
| a |
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
设a>0且a≠1若logax>1对x∈(0,
)恒成立,则a的取值范围是( )
| π |
| 4 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
不等式(x-3)(x-1)<0的解集是( )
| A、{x|1<x<3} |
| B、{x|x<1或x>3} |
| C、{x|x<1} |
| D、{x|x>3} |
 如图为80辆汽车通过某一段公路时的时速的频率分布直方图,则时速大于60的汽车大约有
如图为80辆汽车通过某一段公路时的时速的频率分布直方图,则时速大于60的汽车大约有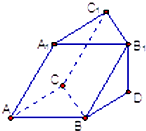 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )