题目内容
“x∈{3,a}”是不等式2x2-5x-3≥0成立的一个充分不必要条件,则实数a的取值范围是( )
| A、(3,+∞) | ||
B、(-∞,-
| ||
C、(-∞,-
| ||
D、(-∞,-
|
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由不等式2x2-5x-3≥0,解得x≥3或x≤-
.再利用充分不必要条件的意义即可得出.
| 1 |
| 2 |
解答:
解:由不等式2x2-5x-3≥0,解得x≥3或x≤-
.
∵“x∈{3,a}”是不等式2x2-5x-3≥0成立的一个充分不必要条件,
∴a>3或a≤-
.
故选:D.
| 1 |
| 2 |
∵“x∈{3,a}”是不等式2x2-5x-3≥0成立的一个充分不必要条件,
∴a>3或a≤-
| 1 |
| 2 |
故选:D.
点评:本题考查了一元二次不等式的解法、充分必要条件,属于基础题.

练习册系列答案
相关题目
在△ABC中,
=
,
=
,
=
,且满足:|
|=1,|
|=2,|
|=
,则
•
+
•
+
•
的值为( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| c |
| 3 |
| a |
| b |
| b |
| c |
| c |
| a |
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
设a>0且a≠1若logax>1对x∈(0,
)恒成立,则a的取值范围是( )
| π |
| 4 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
等比数列{an},满足a1=2,公比q=2,则a5=( )
| A、10 | B、16 | C、32 | D、64 |
有一段演绎推理:“因为对数函数y=logax是减函数;已知y=log2x是对数函数,所以y=log2x是减函数”,结论显然是错误的,这是因为( )
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
为了得到函数y=sin(
x-
)的图象,只需将y=sin
x图象上的每个点纵坐标不变,横坐标( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
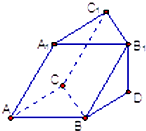 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )